Lagrange-multiplicator

De methode van de lagrange-multiplicatoren is een techniek uit de wiskunde, in het bijzonder uit de wiskundige optimalisatie, om een optimaliseringsprobleem met nevenvoorwaarden op te lossen. Daarbij is een lagrange-multiplicator een bepaald soort hulpvariabele die bij deze techniek wordt ingevoerd, waarmee zowel de formulering als de oplossing van het optimalisatieprobleem sterk vereenvoudigd wordt. De methode is genoemd naar de Italiaanse wiskundige Joseph Louis Lagrange.

Uitleg

Afbeelding 1: Zoek de $x$ en $y$ waarvoor de functie $f(x,y)$ maximaal is, en waarvoor de eis $g(x,y)=c$ (weergegeven in het rood) voldaan is.

{\displaystyle x} — Afbeelding 1: Zoek de $x$ en $y$ waarvoor de functie $f(x,y)$ maximaal is, en waarvoor de eis $g(x,y)=c$ (weergegeven in het rood) voldaan is.

Veel optimaliseringsproblemen zijn van de vorm:

maximaliseer de functie

f(x,y)

onder de voorwaarde

g(x,y)=c

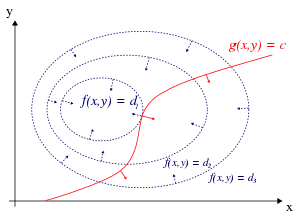
In woorden: zoek het punt $(x,y)$ dat op de kromme $g(x,y)=c$ ligt en waarvoor de functie $f$ maximaal is. Dit probleem is geschetst op de afbeeldingen rechts.

Als uit de voorwaarde afgeleid kan worden hoe een van de variabelen afhankelijk is van de andere, bijvoorbeeld $y=y(x)$ , kan deze relatie gesubstitueerd worden in de te maximaliseren functie, zodat het probleem slechts één variabele heeft:

maximaliseer

f(x,y(x))

Als dit niet het geval is kan het probleem soms opgelost worden door de invoering van een nieuwe variabele $\lambda$ , de zogeheten Lagrange-multiplicator, en de functie $\Lambda ,$ Lagrangefunctie genoemd, te beschouwen, gedefinieerd door:

\Lambda (x,y,\lambda )=f(x,y)+\lambda {\Big (}c-g(x,y){\Big )}

Het blijkt nu dat er voor een oplossing $(x,y)$ van het oorspronkelijke probleem, noodzakelijk een $\lambda$ bestaat waarvoor $(x,y,\lambda )$ een stationair punt is van de functie $\Lambda (x,y,\lambda )$ .

Deze nieuwe formulering van het probleem heeft twee voordelen: het oorspronkelijke probleem wordt herleid tot een volkomen standaard en goed bestudeerd probleem, namelijk het zoeken naar de stationaire punten van een functie, en verder blijken de op te lossen vergelijkingen in deze formulering in veel gevallen eenvoudiger dan in de oorspronkelijke verwoording.

Intuïtieve uitleg

Afbeelding 2: Alternatieve weergave van afbeelding 1. De rode lijn in het xy-vlak geeft weer de punten die aan de eis $g(x,y)=c$ voldoen, en de waarde van de functie $f(x,y)$ is nu als hoogte weergegeven. De blauwe lijnen zijn hoogtelijnen, dus lijnen waarlangs de waarde van $f$ constant is. De oplossing is gegeven door de plaats waar de rode lijn raakt aan de blauwe hoogtelijn.

{\displaystyle g(x,y)=c} — Afbeelding 2: Alternatieve weergave van afbeelding 1. De rode lijn in het xy-vlak geeft weer de punten die aan de eis $g(x,y)=c$ voldoen, en de waarde van de functie $f(x,y)$ is nu als hoogte weergegeven. De blauwe lijnen zijn hoogtelijnen, dus lijnen waarlangs de waarde van $f$ constant is. De oplossing is gegeven door de plaats waar de rode lijn raakt aan de blauwe hoogtelijn.

Hierboven werd gesteld dat elke oplossing van het oorspronkelijke variatieprobleem gegeven is door een stationair punt van de Lagrangefunctie $\Lambda$ . (Andersom is dit niet waar: niet elk stationair punt van $\Lambda$ geeft een oplossing van het oorspronkelijke variatieprobleem.) Om deze uitspraak intuïtief te begrijpen, kan men de volgende redenering houden. Beschouw de lijnen waarlangs de functie $f$ een constante waarde heeft: $f(x,y)=d$ . Als men de functiewaarden van $f$ op de z-as aangeeft, zijn deze lijnen de hoogtelijnen. Er zijn er zo twee getekend op de afbeelding rechts (dat wil zeggen, voor twee verschillende functiewaarden $d_{1}$ en $d_{2}$ ). Stel nu dat we wandelen langs de rode kromme $g(x,y)=c$ . Dat is de verzameling punten die aan het vereiste voldoen. In het algemeen zal (gedurende dit wandelen) de waarde van $f$ aan het toe-, dan wel afnemen zijn. Dat wil zeggen dat op die plaatsen de kromme de hoogtelijnen snijdt. Echter, op het punt van de kromme waar $f$ extreem is, verandert de hoogte niet meer (bereikt zijn minimum/maximum), en dus raakt de hoogtelijn daar de kromme $g(x,y)=c$ . Aangezien de gradiënt van een functie loodrecht staat op de lijnen waarlangs deze functie constant is, impliceert de vorige zin dat ter hoogte van het gezochte punt – d.w.z. het punt waar $f(x,y)$ extremaal en $g(x,y)=c$ geldt – de gradiënten van $f$ en $g$ evenwijdig zijn. De oplossing van het probleem heeft dus als bijzondere eigenschap

\left({\frac {\partial f}{\partial x}},{\frac {\partial f}{\partial y}}\right)=-\lambda \left({\frac {\partial g}{\partial x}},{\frac {\partial g}{\partial y}}\right)

Hier drukt de constante $\lambda$ uit dat de loodrecht op de hoogtelijnen staande vectoren (de gradiënten) evenwijdig aan elkaar zijn, maar niet noodzakelijk even groot zijn/in dezelfde richting wijzen.

Nu zien we dat de uitspraak in de voorgaande sectie inderdaad steek houdt. Daar werd gesteld dat de oplossing van het probleem gegeven is door stationaire punten van de Lagrangefunctie, dus punten waarvoor

\nabla _{x,y,\lambda }\Lambda (x,y,\lambda )=0

(de notatie $\nabla _{x,y,\lambda }$ slaat weer op de gradiënt, dus zowel de afgeleiden naar $x$ , en naar $y$ , als die naar $\lambda$ moeten nul zijn.) Als we de uitdrukking voor de Lagrangefunctie $\Lambda$ invullen, zien we dat de afgeleiden naar $x$ en $y$ impliceren dat

\nabla _{x,y}f=-\lambda \nabla _{x,y}g

Dat is precies de bovenstaande uitspraak dat ter hoogte van de oplossing, de loodrechte vectoren op de hoogtelijnen van $f$ en $g$ evenwijdig zijn. Anderzijds, de afgeleide naar $\lambda$ geeft het oorspronkelijke vereiste, namelijk

g(x,y)=c

Dit bevestigt (ten minste intuïtief) dat elke oplossing $(x,y)$ van het oorspronkelijke probleem overeenkomt met een $(x,y,\lambda )$ die voldoet aan $\nabla \Lambda =0$ .

Typisch vindt men echter een aantal oplossingen voor $\nabla \Lambda =0$ , waarvan dan slechts een of enkele oplossingen voldoen aan het oorspronkelijke probleem. (Dit is analoog aan het zoeken naar extrema van een functie. De punten waar de afgeleide van de functie nul worden zijn lokale extrema, en typisch zijn daarvan slechts een of twee punten globale extrema.)

Eenvoudig voorbeeld

Voor welk(e) punt(en) op de eenheidscirkel is de som van de coördinaten maximaal? Voor dit probleem is $f(x,y)=x+y$ de functie die gemaximaliseerd moet worden, onder de voorwaarde $g(x,y)=x^{2}+y^{2}=1=c$ . Aangezien de lijnen van constante $x+y$ gegeven zijn door rechtes, met richtingscoëfficiënt $-1$ , kan men vrijwel op het eerste gezicht zien dat de raakpunten tussen een van deze hoogtelijnen en de cirkel zijn gegeven door de punten $({\tfrac {1}{2}}{\sqrt {2}},{\tfrac {1}{2}}{\sqrt {2}})$ en $(-{\tfrac {1}{2}}{\sqrt {2}},-{\tfrac {1}{2}}{\sqrt {2}})$ . Het eerste van de twee is het punt waarin $f$ maximaal is.

De oplossing met een Lagrange-multiplicator gaat als volgt.

De Lagrange-functie is

\Lambda (x,y,\lambda )=f(x,y)+\lambda (c-g(x,y))=x+y+\lambda (1-x^{2}-y^{2})

Stel de afgeleiden van $\Lambda$ naar $x$ en naar $y$ gelijk aan 0:

{\frac {\partial \Lambda }{\partial x}}=1-2\lambda x=0

{\frac {\partial \Lambda }{\partial y}}=1-2\lambda y=0

De afgeleide naar $\lambda$ levert weer de voorwaarde

x^{2}+y^{2}=1

De eerste twee vergelijkingen impliceren dat $x=y$ , en als men dit in de voorwaarde invult, volgt dat $2x^{2}=1$ ; dus $x=\pm {\tfrac {1}{2}}{\sqrt {2}}$ .

De punten waarin $f$ een extreme waarde aanneemt, zijn dus $({\tfrac {1}{2}}{\sqrt {2}},{\tfrac {1}{2}}{\sqrt {2}})$ en $(-{\tfrac {1}{2}}{\sqrt {2}},-{\tfrac {1}{2}}{\sqrt {2}})$ . Niet elk extremaal van de Lagrange-functie is een oplossing van het oorspronkelijke probleem. Het maximum van $x+y$ wordt bereikt voor de eerste van deze twee mogelijkheden.

Betekenis van de multiplicatoren, toepassingen in de economie

Bij veel problemen heeft de concrete waarde van de Lagrange-multiplicator ook een betekenis. Bedenk eerst dat:

-{\frac {\partial \Lambda }{\partial c}}=\lambda

$\lambda$ drukt uit in welke mate het maximum verandert indien men in de voorwaarde $g(x,y)=c$ de waarde van $c$ verandert. In de economie gebuikt men Lagrange-multiplicatoren voor vraagstukken van de vorm: gegeven een bepaald budget, hoe kan een bepaalde grootheid (bijv. het economisch nut) dit maximaliseren. De Lagrange-multiplicator geeft dan aan in welke mate de grootheid verandert als men de voorwaarde wijzigt.