Cosinusregel

In de goniometrie beschrijft de cosinusregel een relatie tussen de drie zijden van een driehoek en de cosinus van een hoek.

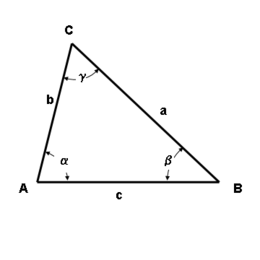
Voor de driehoek in de figuur kan de cosinusregel voor elk van de zijden worden geformuleerd:

${\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos \gamma }$

en dus ook:

${\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos \alpha }$

${\displaystyle b^{2}=c^{2}+a^{2}-2ca\cos \beta }$

Omgevormd naar de hoek wordt dit:

${\displaystyle \alpha =\arccos \left({\frac {b^{2}+c^{2}-a^{2}}{2bc}}\right)}$

${\displaystyle \beta =\arccos \left({\frac {a^{2}+c^{2}-b^{2}}{2ac}}\right)}$

${\displaystyle \gamma =\arccos \left({\frac {a^{2}+b^{2}-c^{2}}{2ab}}\right)}$

De regel kan met de congruentiestellingen voor driehoeken en de sinusregel worden gebruikt om de lengtes van de zijden en de hoeken in een driehoek te berekenen. Is ${\displaystyle \gamma }$ een rechte hoek, dus 90°, dan is ${\displaystyle \cos \gamma =0}$ en vervalt de cosinusregel tot ${\displaystyle c^{2}=a^{2}+b^{2}}$, de stelling van Pythagoras. De cosinusregel is in feite gelijk aan de projectiestelling.

Toepassingen

De cosinusregel kan onder andere worden toegepast

• om een hoek te berekenen als de drie zijden bekend zijn, congruentiestelling ZZZ en
• om de derde zijde te berekenen, als twee zijden en de door deze zijden ingesloten hoek bekend zijn, congruentiestelling ZHZ.

Congruentiestellingen voor een driehoek

De congruentiestellingen ZZZ zijde-zijde-zijde en ZHZ zijde-hoek-zijde geven aan, dat een driehoek volledig bepaald is, zodra alle drie de zijden ZZZ of twee zijden en de daardoor ingesloten hoek ZHZ bekend zijn. Het is met de cosinusregel in deze gevallen mogelijk met deze drie gegevens in het geval van ZZZ de drie hoeken en in het geval van ZHZ de lengte van de derde zijde te berekenen en met behulp van de sinusregel de twee andere hoeken te berekenen.

Als er slechts een zijde en twee hoeken, de congruentiestellingen ZHH of HZH, of twee zijden en de tegenoverliggende hoek van de grootste zijde, congruentiestelling ZzH, bekend zijn, kan men eerst een van de ontbrekende hoeken met de sinusregel berekenen, waarna de ook derde hoek bekend is. De som van de drie hoeken in een driehoek is gelijk aan 180°. Afsluitend kan men de cosinusregel toepassen om de derde zijde te bepalen.

Bewijs

Er bestaan verschillende bewijzen van de cosinusregel. Er worden er hier drie genoemd.

Directe afleiding

Vanuit ${\displaystyle C}$ is de loodlijn ${\displaystyle d}$ neergelaten op de zijde ${\displaystyle c}$. Zoals men in de figuur kan zien, verdeelt de loodlijn ${\displaystyle d}$ de driehoek in twee rechthoekige driehoeken. Volgens de stelling van Pythagoras geldt:

${\displaystyle b^{2}=d^{2}+e^{2}}$

en

${\displaystyle a^{2}=d^{2}+(c-e)^{2}}$

Eliminatie van ${\displaystyle d^{2}}$ geeft:

${\displaystyle a^{2}=b^{2}+c^{2}-2ce}$

Verder is:

${\displaystyle \cos(\alpha )=e/b}$, waaruit volgt ${\displaystyle e=b\cos(\alpha )}$

Beide formules gecombineerd geeft:

${\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos(\alpha )}$

Vectorformulering

Beschouw de zijden van de driehoek als vectoren en noem:

${\displaystyle {\vec {a}}={\overrightarrow {BC}},\ {\vec {b}}={\overrightarrow {AC}},\ {\vec {c}}={\overrightarrow {AB}}}$

Dan is:

${\displaystyle {\vec {c}}={\vec {b}}-{\vec {a}}}$,

zodat met het inwendig product van twee vectoren volgt:

${\displaystyle c^{2}=\|{\vec {c}}\|^{2}=\|{\vec {b}}-{\vec {a}}\|^{2}=({\vec {b}}-{\vec {a}})\cdot ({\vec {b}}-{\vec {a}})=\|{\vec {b}}\|^{2}+\|{\vec {a}}\|^{2}-2\,{\vec {a}}\cdot {\vec {b}}=b^{2}+a^{2}-2ab\cos \gamma }$

De laatste gelijkheid volgt uit de definitie van de hoek tussen twee vectoren.

Vergelijking van oppervlakten

Een ander bewijs gaat door vergelijking van oppervlakten. Denk daarbij aan tangram. We moeten onderscheid maken in het geval met scherpe hoek ${\displaystyle \gamma }$ en het geval met stompe hoek ${\displaystyle \gamma }$. Beide mogelijkheden worden met een figuur geïllustreerd.

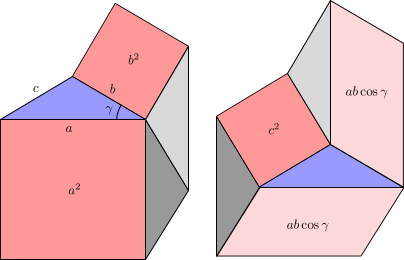
Geval met scherpe hoek ${\displaystyle \gamma }$

Een zevenhoek is verdeeld in:

• de roze oppervlakten ${\displaystyle a^{2},\ b^{2}}$ links en ${\displaystyle 2ab\cos \gamma }$ en ${\displaystyle c^{2}}$ rechts
• de driehoek ABC in het blauw
• grijze hulpdriehoeken alle congruent met driehoek ABC.

Uit vergelijking van de oppervlakten links en rechts blijkt:

${\displaystyle a^{2}+b^{2}=c^{2}+2ab\cos \gamma }$

waaruit de cosinusregel volgt.

Geval met stompe hoek ${\displaystyle \gamma }$

Een zeshoek is verdeeld in:

• de roze oppervlakten ${\displaystyle a^{2},\ b^{2}}$ en ${\displaystyle -2ab\cos \gamma }$ links en ${\displaystyle c^{2}}$ rechts
• twee keer in het blauw met driehoek ABC congruente driehoeken

Uit vergelijking van de oppervlakten links en rechts volgt direct de cosinusregel:

${\displaystyle a^{2}+b^{2}-2ab\cos \gamma =c^{2}}$

Zie de categorie Law of cosines van Wikimedia Commons voor mediabestanden over dit onderwerp.