Momento polar de inércia

O momento polar de inércia (em inglês: polar moment of inertia), também conhecido como segundo momento polar de área, é uma quantidade usada para descrever resistência à deformação torcional em objetos cilíndricos (ou segmentos de objetos cilíndricos) com uma seção transversal invariante e sem empenamento (deformação fora do plano) significativo.^[1] É um constituinte do momento de inércia de área, relacionados através do Teorema dos eixos perpendiculares. Onde o segundo momento de área planar descreve a resistência de um objeto à deflexão quando submetido a uma força aplicada a um plano paralelo ao eixo central, o segundo momento de área polar descreve a resistência de um objeto à rotação quando submetido a um momento aplicado em um plano perpendicular ao eixo central de um objeto. Similar ao segundo momento de área planar (${\displaystyle I_{x}}$,${\displaystyle I_{y}}$ e ${\displaystyle I_{xy}}$), o segundo momento de área polar é frequentemente denotado como ${\displaystyle I_{z}}$. Enquanto diversos livros-texto de engenharia e publicações acadêmicas também o denotem como ${\displaystyle J}$ ou ${\displaystyle J_{z}}$, deve-se prestar atenção cuidadosa tal que ela não seja confundida com o módulo de torção ${\displaystyle J_{t}}$, usado para objetos não-cilíndricos.

De forma simples, o momento polar de inércia é a resistência de um eixo ou viga de ser distorcido por torção, em função de sua forma. A rigidez vem apenas da área transversal do objeto e não depende da composição do material ou módulo de cisalhamento. Quanto maior a magnitude do momento polar de inércia, maior a resistência à torção do objeto.

Definição

Nota: Embora tenha se tornado comum encontrar o termo momentos de inércia usado para descrever os segundos momentos de área polar e planar , isso é principalmente uma construção de campos de engenharia. O termo momento de inércia, dentro dos campos da física e da matemática, é estritamente o momento de inércia de massa, ou segundo momento de massa, usado para descrever a resistência de um objeto maciço ao movimento rotacional, não sua resistência à deformação torcional. Enquanto os segundos momentos de inércia polar e planar são integrados sobre todos os elementos infinitesimais de uma determinada área em alguma seção transversal bidimensional, o momento de inércia de massa é integrado sobre todos os elementos infinitesimais de massa em um espaço tridimensional ocupado por um objeto. Simplificando, os segundos momentos de inércia polar e planar são uma indicação de rigidez, e o momento de inércia de massa é a resistência ao movimento rotacional de um objeto massivo.

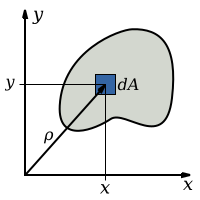
A equação que descreve o momento polar de inércia é uma integral múltipla sobre a área da seção transversal, ${\displaystyle A}$, do objeto.

${\displaystyle J=\iint \limits _{A}\rho ^{2}dA}$

onde ${\displaystyle \rho }$ é a distância ao elemento ${\displaystyle dA}$.

Substituindo as componentes ${\displaystyle x}$ e ${\displaystyle y}$, usando o teorema de Pitágoras

${\displaystyle J=\iint \limits _{A}(x^{2}+y^{2})dxdy}$

${\displaystyle J=\iint \limits _{A}x^{2}dxdy+\iint \limits _{A}y^{2}dxdy}$

Dadas as equações do segundo momento de inércia planar

${\displaystyle I_{x}=\iint \limits _{A}y^{2}dxdy}$

${\displaystyle I_{y}=\iint \limits _{A}x^{2}dxdy}$

o momento de inércia polar pode ser descrito como a soma dos momentos de inércia planar ${\displaystyle x}$ e ${\displaystyle y}$, ${\displaystyle I_{x}}$ e ${\displaystyle I_{y}}$

${\displaystyle \therefore J=I_{z}=I_{x}+I_{y}}$

Isto é mostrado no teorema dos eixos perpendiculares.^[2] Para objetos que tem simetria rotacional, tal como um cilindro ou tubo vazado, a equação pode ser simplificada na forma

${\displaystyle J=2I_{x}}$ ou ${\displaystyle J=2I_{y}}$

Para uma seção circular de raio r:

${\displaystyle J=\int _{0}^{2\pi }\int _{0}^{r}\rho ^{2}\rho \,d\rho \,d\phi ={\frac {\pi r^{4}}{2}}}$

Unidade

A unidade SI para momento polar de inércia, como para o momento de inércia de área, é metro na potência quatro (m⁴).

Referências

Ver também

• Momento de inércia de área
• Módulo de cisalhamento
• Barra de torção

Ligações externas

• Torsion of Shafts - engineeringtoolbox.com
• Elastic Properties and Young Modulus for some Materials - engineeringtoolbox.com
• Material Properties Database - matweb.com