YBC 7289

YBC 7289 – gliniana tabliczka(inne języki) babilońska słynna z tego, że z dużą dokładnością określa przybliżenie pierwiastka kwadratowego z 2 zapisanego w systemie sześćdziesiątkowym, który jest długością przekątnej kwadratu jednostkowego. Precyzja zapisu tej liczby jest równoważna zapisowi dziesiętnemu z 6 cyframi znaczącymi. Tabliczka jest przypuszczalnie dziełem ucznia z południowej Mezopotamii z czasów między 1800–1600 p.n.e. Znajduje się ona w zbiorach Yale Babylonian Collection(inne języki) dzięki darowiźnie J.P. Morgana.

Opis

Tabliczka przedstawia kwadrat z dwiema przekątnymi oraz trzy liczby

Zapis babiloński	Dziesiętne wartości cyfr	Pozycja na tabliczce
	30	bok kwadratu
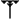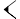	1   24   51   10	przekątna kwadratu
	42   25   35	pod tą samą przekątną

Odwrotna strona jest częściowo wytarta. Prawdopodobnie zawiera ona podobny problem rozważający prostokąt, którego dwa boki i przekątna są w stosunku 3:4:5^[1]

Średnica tabliczki to około 8 cm^[2] .

Historia

Dokładne pochodzenie tabliczki YBC 7289 nie jest znane. Jej kształt i styl zapisu mogą wskazywać, że powstała na terenach południowej Mezopotamii (obecnie Irak) w latach między 1800–1600 p.n.e.^[2] [3] lub nawet 1900 p.n.e.^[4]

Od 1909 tabliczka znajduje się w zasobach uniwersytetu Yale dzięki darowiźnie J.P. Morgana, który przekazał tam swoją kolekcję tabliczek babilońskich, co dało początek Yale Babylonian Collection(inne języki)^[5] .

Dzięki współpracy instytutów w Yale, jednego odpowiedzialnego za zachowanie dziedzictwa kulturowego i drugiego od innowacyjnych projektów, powstał cyfrowy model tabliczki odpowiedni do drukowania przestrzennego^[5] [6] .

Interpretacja

Niewielki zaokrąglony kształt tabliczki i duże napisy na niej sugerują, że była to „tabliczka podręczna”, typowa do domowych ćwiczeń, używana przez ucznia, który trzyma ją w dłoni^[7].

Liczby zapisane są systemie sześćdziesiątkowym a ich wartości można wyznaczyć w następujący sposób^[4]:

${\displaystyle \mathbf {1} +{\frac {\mathbf {24} }{60}}+{\frac {\mathbf {51} }{60^{2}}}+{\frac {\mathbf {10} }{60^{3}}}={\frac {305470}{216000}}\approx 1{,}41421296}$

${\displaystyle \mathbf {42} +{\frac {\mathbf {25} }{60}}+{\frac {\mathbf {35} }{60^{2}}}={\frac {152735}{3600}}\approx 42{,}4263889}$

Trzy liczby z tabliczki łączy relacja ${\displaystyle 30\times 1{,}41421296\approx 42{,}4263889}$^[8][9].

Znaczenie matematyczne tej tabliczki zauważyli Otto E. Neugebauer(inne języki) i Abraham Sachs(inne języki) w 1945^[2] [10]. Na tabliczce znajduje się najstarsze znane przybliżenie liczby ${\displaystyle {\sqrt {2}}}$^[11], a rysunek kwadratu i przekątnych dowodzi, że Babilończycy znali twierdzenie Pitagorasa^[12]. Tabliczka ta „przedstawia największą znaną i kiedykolwiek uzyskaną dokładność obliczeniową świata starożytnego”, równoważną sześciu dziesiętnym cyfrom znaczącym^[2] . Wysoka dokładność numeryczna na tabliczce YBC 7289 uświadamia, że są to wyniki jakiejś ogólnej metody ich obliczania, niż jedynie szacowania^[13].

Takie samo przybliżenie ${\displaystyle {\sqrt {2}},}$ używając liczb 1, 24, 51 i 10 zastosował dużo później grecki matematyk Klaudiusz Ptolemeusz w swoim dziele Almagest^[14][15]. Ptolemeusz nie wyjaśnia, skąd to przybliżenie pochodzi, więc zakłada się, że było ono wówczas dobrze znane^[16].

Z uwagi na znaczenie liczb odwrotnych w matematyce babilońskiej, istnieje alternatywna interpretacja liczby 30 jako „0 30”, czyli ułamka ${\displaystyle 1/2,}$ a stąd „0 42 25 35” to ${\displaystyle 1/{\sqrt {2}}\approx 0{,}7071064817.}$ Zatem na tabliczce może znajdować się para liczb odwrotnych wraz z ich geometryczną interpretacją^[17].

Przypisy

Bibliografia

• Janet L.J.L. Beery Janet L.J.L., Frank J.F.J. Swetz Frank J.F.J., The best known old Babylonian tablet?, „Convergence”, Mathematical Association of America, 2012, DOI: 10.4169/loci003889 .
• DavidD. Fowler DavidD., EleanorE. Robson EleanorE., Square Root Approximations in Old Babylonian Mathematics. YBC 7289 in Context, „Historia Mathematica”, 25 (4), 1998, s. 366–378, DOI: 10.1006/hmat.1998.2209  (ang.).
• PatrickP. Lynch PatrickP., A 3,800-year journey from classroom to classroom, „Yale News”, 11 kwietnia 2016 [dostęp 2020-05-01] .
• Otto E.O.E. Neugebauer Otto E.O.E., A History of Ancient Mathematical Astronomy, Part One, Springer-Verlag, New York-Heidelberg, 1975, ISBN 978-3-642-61910-6 .
• Otto E.O.E. Neugebauer Otto E.O.E., AbrahamA. Sachs AbrahamA., Mathematical Cuneiform Texts, American Oriental Society and the American Schools of Oriental Research, New Haven, Conn., 1945 (American Oriental Series) .
• OlafO. Pedersen OlafO., A Survey of the Almagest, AlexanderA. Jones (red.), Springer, 2011 (Sources and Studies in the History of Mathematics and Physical Sciences), ISBN 978-0-387-84826-6 .
• BenoîtB. Rittaud BenoîtB., Le fabuleux destin de √2, Paris: Le Pommier, 2006, ISBN 2-74650275-5  (fr.).
• EleanorE. Robson EleanorE., Mesopotamian Mathematics, [w:] Victor J.V.J. Katz (red.), The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook, Princeton University Press, 2007, ISBN 978-3-642-61910-6 .
• Peter S.P.S. Rudman Peter S.P.S., How mathematics happened: the first 50,000 years, Prometheus Books, Amherst, NY, 2007, ISBN 978-1-59102-477-4 .
• IanI. Stewart IanI., 17 równań które zmieniły świat, Warszawa: Prószyński i S-ka, 2013, ISBN 978-83-7839-628-4 .
• A 3D-print of ancient history: one of the most famous mathematical texts from Mesopotamia, Yale Institute for the Preservation of Cultural Heritage, 16 stycznia 2016 [dostęp 2020-05-01] , (skrót: IPCH).
• Matematyka, Warszawa: Wydawnictwa Szkolne i Pedagogiczne, 1990 (Encyklopedia szkolna), ISBN 83-02-02551-8 .