Iloczyn tensorowy modułów

Iloczynem tensorowym modułów ${\displaystyle M}$ i ${\displaystyle N}$ nazywa się taki moduł, którego odwzorowania liniowe (homomorfizmy) w dowolny moduł ${\displaystyle Z}$ są we wzajemnie jednoznacznej odpowiedniości z odwzorowaniami dwuliniowymi modułów ${\displaystyle M}$ i ${\displaystyle N}$ w moduł ${\displaystyle Z.}$

Istnienie i określenie

Jeżeli ${\displaystyle R}$ jest pierścieniem przemiennym oraz ${\displaystyle M}$ i ${\displaystyle N}$ są odpowiednio prawym i lewym ${\displaystyle R}$-modułem, to istnieje z dokładnością do izomorfizmu jedyny taki ${\displaystyle R}$-moduł ${\displaystyle P}$ oraz odwzorowanie dwuliniowe

${\displaystyle \theta \colon M\times N\to P,}$

że dla każdej grupy abelowej ${\displaystyle Z}$ oraz dla każdego odwzorowania dwuliniowego

${\displaystyle f\colon M\times N\to Z}$

istnieje taki homomorfizm grup

${\displaystyle {\tilde {f}}\colon P\to Z,}$

że

${\displaystyle {\tilde {f}}\circ \theta =f.}$

Moduł ${\displaystyle P}$ (wraz z odzorowaniem ${\displaystyle \otimes :=\theta }$) nazywana jest iloczynem tensorowym modułów ${\displaystyle M}$ i ${\displaystyle N}$ i oznaczana symbolem ${\displaystyle M\otimes _{R}N}$ (bądź po prostu ${\displaystyle M\otimes N,}$ gdy z kontekstu wynika nad jakim pierścieniem ${\displaystyle R}$ rozważane są moduły). Innymi słowy, iloczyn tensorowy ${\displaystyle M}$ i ${\displaystyle N}$ to jedyna z dokładnością do izomorfizmu grupa abelowa ${\displaystyle M\otimes _{R}N,}$ dla której diagram

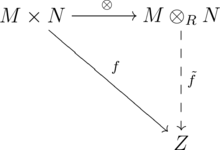
jest przemienny.

Konstrukcja iloczynu tensorowego modułów

Iloczyn tensorowy ${\displaystyle R}$-modułów ${\displaystyle M}$ i ${\displaystyle N}$ (wraz z odwzorowaniem ${\displaystyle \theta =\otimes _{R}}$) może zostać skonstruowany w następujący sposób: rozpatrzmy moduł wolny ${\displaystyle F(M\times N)}$ generowany przez iloczyn kartezjański ${\displaystyle M\times N.}$ Jego elementami są funkcje ${\displaystyle f\colon M\times N\to R}$ o skończonym nośniku ${\displaystyle \operatorname {supp} f:=\{x\in M\times N;\ f(x)\neq 0\}}$ postaci

${\displaystyle f=\sum _{(m,n)\in M\times N}r_{(m,n)}(m,n)}$

dla pewnych ${\displaystyle r_{(m,n)}\in R,}$ gdzie ${\displaystyle (m,n)\in F(M\times N)}$ oznacza funkcję, która ${\displaystyle (x,y)\in M\times N}$ przyporządkowuje 1, gdy ${\displaystyle (x,y)=(m,n)\in M\times N}$ i 0 w przeciwnym wypadku. Moduł ilorazowy

${\displaystyle F(M\times N)/S,}$

gdzie ${\displaystyle S}$ jest podmodułem modułu ${\displaystyle F(M\times N),}$ generowanym przez elementy postaci

${\displaystyle (rm+r'm',n)-r(m,n)-r'(m',n),}$

${\displaystyle (m,rn+r'n')-r(m,n)-r'(m,n'),}$

dla ${\displaystyle m,m'\in M,n,n'\in N,r,r'\in R,}$ jest iloczynem tensorowym modułów ${\displaystyle M}$ i ${\displaystyle N{:}}$

${\displaystyle F(M\times N)/S=M\otimes _{R}N.}$

Element

${\displaystyle m\otimes _{R}n:=(m,n)+S}$

nazywany jest tensorem prostym elementów ${\displaystyle m\in M}$ i ${\displaystyle n\in N,}$ a każdy element ${\displaystyle M\otimes _{R}N}$ – tensorem. Zbiór wszystkich tensorów prostych jest zbiorem wolnych generatorów iloczynu tensorowego ${\displaystyle M\otimes _{R}N.}$ Tensor prosty ${\displaystyle m\otimes _{R}n}$ jest obrazem pary ${\displaystyle (m,n)}$ w homomorfizmie kanonicznym

${\displaystyle \pi \colon F(M\times N)\to F(M\times N)/S=M\otimes _{R}N.}$

Jeżeli ${\displaystyle M_{1},...,M_{n}}$ są ${\displaystyle R}$-bimodułami, to można wprowadzić definicję iloczynu tensorowego

${\displaystyle M_{1}\otimes _{R}\ldots \otimes _{R}M_{n},}$

zastępując odpowiednio odwzorowania dwuliniowe odwzorowaniami ${\displaystyle n}$-liniowymi w określeniu.

Zobacz też

• iloczyn tensorowy przestrzeni liniowych
• iloczyn tensorowy macierzy
• iloczyn tensorowy przestrzeni Banacha
• iloczyn tensorowy przestrzeni Hilberta

Bibliografia

• Claude Chevalley, Fundamental concepts of algebra. New York, Academic Press, 1956. s. 74–77.