Det annet arealmoment

Denne artikkelen mangler kildehenvisninger, og opplysningene i den kan dermed være vanskelige å verifisere. Kildeløst materiale kan bli fjernet. Helt uten kilder. (10. okt. 2015)

Det annet arealmoment (I, ofte feilaktig kalt treghetsmomentet; I denne sammenhengen handler det om arealtreghetsmomentet, og ikke massetreghetsmomentet som brukes i dynamikk. Se treghetsmoment.) beregnes for bjelketverrsnitt og andre geometriske former, ved integrasjon over tverrsnittet:

${\displaystyle I=\int \limits _{A}y^{2}\,dA}$

I vanlig praksis brukes formler som er beregnet for standardprofiler, og noen eksempler er gitt under.

Rektangulært tverrsnitt

Integralet løses på følgende måte for et rektangulært tverrsnitt:

${\displaystyle I_{x}=\int \limits _{-h/2}^{h/2}y^{2}\,bdy={\left[{\frac {y^{3}b}{3}}\right]}_{-h/2}^{h/2}={\frac {bh^{3}}{12}}}$

der h er høyden, og b er bredden av det rektangulære tverrsnittet. I_x blir da annet arealmoment om x-aksen i senteret C.

Sirkulært tverrsnitt

Integralet er ikke vist her, men et rørtverrsnitt beregnes fra ${\displaystyle I={\frac {\pi D^{4}}{64}}}$, der D er ytterdiameteren

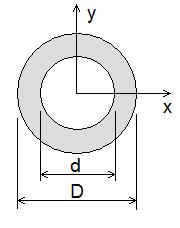
Rørtverrsnitt

${\displaystyle I={\frac {\pi }{64}}(D^{4}-d^{4})}$

der D er ytterdiameteren, og d er innerdiameteren.

Steiners teorem

Dersom du har et tverrsnitt som er sammensatt av flere arealer som ikke ligger på samme akse som tyngdepunktet av arealet, er det vanlig å bruke Steiners teorem for å beregne annet arealmoment, kalt parallellakseteoremet, eller Steiners Sats.

${\displaystyle I_{z}=I_{x}+Ad^{2}.\,}$, der I_x er annet arealmoment for arealet som ligger på en parallell akse utenfor arealsenteret (i akse z), d er avstanden fra arealsenteret i akse z til arealsenteret av A.

Anvendelse av annet arealmoment

En vanlig anvendelse av annet arealmoment er ved beregning av bøyespenningen, ${\displaystyle \sigma _{b}}$ i en bjelke.

${\displaystyle \sigma _{b}={\frac {M}{I}}y}$

der M er momentet, I er annet arealmoment og y er avstanden fra arealsenteret til punktet der du ønsker å beregne spenningen.

Motstandsmomentet

Et annet vanlig begrep i bjelkeberegninger er motstandsmomentet eller tverrsnittsmodulen (Engelsk: Section modulus), og benevnes ofte W. I vanlig praksis beregnes største bøyespenning ${\displaystyle \sigma _{b}}$ fra

${\displaystyle \sigma _{b}={\frac {M}{W}}}$, der ${\displaystyle W={\frac {I}{y}}={\frac {I}{h/2}}}$

siden arealsenteret til tverrsnittet vanligvis ligger i midten av tverrsnittet, og følgelig er avstanden fra senteret av tverrsnittet til ytterste fiber lik h/2.

Motstandsmomentet for noen vanlige tverrsnitt er gitt under

Rektangulært tverrsnitt

${\displaystyle W_{x}={\frac {bh^{2}}{6}}}$

b = bredden, h = høyden Her gjelder bøying om x-akse

Sirkulært tverrsnitt

${\displaystyle W={\frac {\pi D^{3}}{32}}}$

D = diameteren

Rørtverrsnitt

${\displaystyle W={\frac {\pi }{32D}}(D^{4}-d^{4})}$

D = ytterdiameter, d = innerdiameter