ベッセル関数(ベッセルかんすう、英: Bessel function)とは、最初にスイスの数学者ダニエル・ベルヌーイによって定義され、フリードリヒ・ヴィルヘルム・ベッセルにちなんで名づけられた関数。円筒関数と呼ばれることもある。以下に示す、ベッセルの微分方程式における の特殊解の1つである。
の特殊解の1つである。

上の式において、 は、任意の実数である(次数と呼ばれる)。
は、任意の実数である(次数と呼ばれる)。 が整数
が整数 に等しい場合がとくに重要である。
に等しい場合がとくに重要である。
 及び
及び はともに同一の微分方程式を与えるが、慣例としてこれら2つの異なる次数に対して異なるベッセル関数が定義される(例えば、
はともに同一の微分方程式を与えるが、慣例としてこれら2つの異なる次数に対して異なるベッセル関数が定義される(例えば、 の関数としてなるべく滑らかになるようにベッセル関数を定義する、など)。
の関数としてなるべく滑らかになるようにベッセル関数を定義する、など)。
そもそもベッセル関数は、惑星の軌道運動に関するケプラー方程式をベッセルが解析的に解いた際に導入された[1]。
応用
ベッセル解はラプラス方程式またはヘルムホルツ方程式の円柱座標系および極座標系における分離解として見出される。従ってベッセル関数は、電波伝播や静電位差などの解を求める際に重要である(円柱座標系においては整数次数  、極座標系においては半整数次数
、極座標系においては半整数次数  のベッセル関数がそれぞれ解として得られる)。例えば、
のベッセル関数がそれぞれ解として得られる)。例えば、
- 円筒導波管における電磁波
- 円柱物体の熱伝導
- 薄い円(か環状の)膜の振動のモード
など。
ベッセル関数はまた、信号処理のような問題で有用な特性を持つ(例えば、FM合成、カイザー窓やベッセルフィルタなど)。
定義
ベッセルの微分方程式は2階の線形微分方程式であるので、線形独立な2つの解が存在するはずである。しかしながら、解を議論する状況に応じて解の様々な表現が便利に使われている。代表的ないくつかの解の表現について以下で説明する。
第1種及び第2種ベッセル関数
これらの関数がベッセル関数群としては最も一般的な形式である。
- 第1種ベッセル関数
- 第1種ベッセル関数は
 と表記される。
と表記される。 はベッセルの微分方程式の解であり、
はベッセルの微分方程式の解であり、 が整数もしくは非負であるとき、
が整数もしくは非負であるとき、 で有限の値をとる。
で有限の値をとる。 における特定解の選択及び正規化は後述する。第1種ベッセル関数はまた、
における特定解の選択及び正規化は後述する。第1種ベッセル関数はまた、 のまわりでのテイラー展開(非整数の
のまわりでのテイラー展開(非整数の  に対しては、より一般にべき級数展開)によって定義することもできる。
に対しては、より一般にべき級数展開)によって定義することもできる。 
非整数の  に対しては、
に対しては、 と
と  とがベッセルの微分方程式に対する線形独立な2つの解を与える。他方で
とがベッセルの微分方程式に対する線形独立な2つの解を与える。他方で が整数の場合には、
が整数の場合には、 という関係が成り立つため、2つの解は線形従属となる。整数次数に対して
という関係が成り立つため、2つの解は線形従属となる。整数次数に対して  と線形独立な第2の解は、第2種ベッセル関数によって与えられる。
と線形独立な第2の解は、第2種ベッセル関数によって与えられる。
- 第2種ベッセル関数
- ノイマン関数
- 第2種ベッセル関数
 はベッセルの微分方程式の解であり
はベッセルの微分方程式の解であり  において特異性を持つ。ベッセル関数はノイマン関数とも呼ばれ、
において特異性を持つ。ベッセル関数はノイマン関数とも呼ばれ、 と表される。
と表される。 - 第2種ベッセル関数と第1種ベッセル関数
 は以下の関係を持つ。
は以下の関係を持つ。 
- ただし、
 が整数のときは右辺は極限によって定義されるものとする。
が整数のときは右辺は極限によって定義されるものとする。
非整数の  に対しては、
に対しては、 と
と  とが線形独立な2つの解を既に与えているので、
とが線形独立な2つの解を既に与えているので、 は解の表現としては冗長である。整数
は解の表現としては冗長である。整数  に対しては、
に対しては、 は
は  と線形独立な第2の解を与えている。 整数
と線形独立な第2の解を与えている。 整数  に対して、
に対して、 と
と  の間に
の間に  という関係が成り立ち、従って両者は線形従属である。
という関係が成り立ち、従って両者は線形従属である。
 及び
及び  はどちらも、負の実軸を除く複素平面上で
はどちらも、負の実軸を除く複素平面上で  の解析的な関数(正則な関数)である。
の解析的な関数(正則な関数)である。 が正の整数のとき、これらの関数は負の実軸上に分岐点を持たず、したがって
が正の整数のとき、これらの関数は負の実軸上に分岐点を持たず、したがって  の整関数となる。また、固定した
の整関数となる。また、固定した  に対して、ベッセル関数は
に対して、ベッセル関数は  の整関数となる。
の整関数となる。
超幾何級数との関係
- ベッセル関数は超幾何級数(超幾何関数ともいう)によって、以下のように表現することができる。

ハンケル関数
- ベッセルの微分方程式に対する線形独立な2つの解を与える表式には、ハンケル関数Hα(1)(x) と Hα(2)(x)があり、定義式は以下の通り。


ここで、 は虚数単位である。
は虚数単位である。 と
と との線形結合によって与えられるこれらの解の表現は、第三種ベッセル関数として知られている(ハンケル関数は円筒波の方程式における、内側もしくは外側への円筒波の伝播の解を表現する)。
との線形結合によって与えられるこれらの解の表現は、第三種ベッセル関数として知られている(ハンケル関数は円筒波の方程式における、内側もしくは外側への円筒波の伝播の解を表現する)。
変形ベッセル関数
ベッセル関数は の複素数値に対しても適切に定義されており、応用上は
の複素数値に対しても適切に定義されており、応用上は  が純虚数の場合が特に重要である。この場合、ベッセルの微分方程式への解は第1種及び第2種の変形ベッセル関数と呼ばれ、以下のように定義される。
が純虚数の場合が特に重要である。この場合、ベッセルの微分方程式への解は第1種及び第2種の変形ベッセル関数と呼ばれ、以下のように定義される。


これらの関数は、 が実数のときに関数値が実数となるように定義されている。またこれらの関数は、変形されたベッセルの微分方程式
が実数のときに関数値が実数となるように定義されている。またこれらの関数は、変形されたベッセルの微分方程式

に対する2つの線形独立な解を与えている。
変形ベッセル関数には以下の性質がある。 ここで、n は正の整数またはゼロ。


球ベッセル関数・球ノイマン関数
第1種及び第2種のベッセル関数から、球ベッセル関数(spherical Bessel functions)と球ノイマン関数(spherical Neumann functions)がそれぞれ以下のように定義される。


これらの関数は、球ベッセル微分方程式
![{\displaystyle {\frac {d^{2}y}{dx^{2}}}+{\frac {2}{x}}{\frac {dy}{dx}}+\left[1-{\frac {\alpha (\alpha +1)}{x^{2}}}\right]y=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dd52b8dbca43b9a94a4cdb7d2bebb90b56f7b9f)
に対する2つの線形独立な解を与えている。
量子力学における3次元自由粒子のシュレーディンガー方程式の動径方向の解のうち、正則なものは球ベッセル関数で表され、正則でないものは球ノイマン関数で表される。
また3次元井戸型ポテンシャルのシュレディンガー方程式における、ポテンシャル内部の動径方向の解のうち、原点で発散しないものは球ベッセル関数で表され、原点で発散するものは球ノイマン関数で表される。
球ハンケル関数
- 球ベッセル微分方程式に対する線形独立な2つの解を与える表式には、球ハンケル関数hα(1)(x) と hα(2)(x)があり、定義式は以下の通り。


ここで、 は虚数単位である。
は虚数単位である。
また、非負の整数 n について:

 は、実数xに関して
は、実数xに関して の複素共役となる。
の複素共役となる。
量子力学では、3次元井戸型ポテンシャルのシュレディンガー方程式における、ポテンシャル外部の動径方向の解は、球ハンケル関数で表される。第一種球ハンケル関数は外向き、第二種球ハンケル関数は内向きを表す。
変形球ベッセル関数
第1種及び第2種の変形ベッセル関数から、変形球ベッセル関数(英:modified spherical Bessel functions)が以下のように定義される。


これらの関数は、変形球ベッセル微分方程式

に対する2つの線形独立な解を与えている。
変形球ベッセル関数には以下の性質がある。

ここで、n は正の整数またはゼロ。
積分表示
Bessel の積分表示[2]

Hansen の積分表示[2]

Poisson の積分表示[2]

Schläfli の積分表示[3]

Schafheitlin の積分表示[4] ただし複号は上が  , 下が
, 下が 
![{\displaystyle {\frac {{\sqrt {\pi }}\Gamma (\nu +1/2)}{z^{\nu }}}H_{\nu }^{(\iota )}(z)=\mp 2^{\nu +1}i\int _{0}^{\pi /2}\exp \left\{\pm i\left[z-\left(\nu -{\frac {1}{2}}\right)\theta \right]-2z\cot \theta \right\}\,\cos ^{\nu -1/2}\theta \,\mathrm {cosec} ^{2\nu +1}\theta \,d\theta \ \ [\mathrm {Re} (\nu )>-{\frac {1}{2}},\ \mathrm {Re} (z)>0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9ff46890d9162f3ac92016f6f35258fcbe20c07)
Heine の積分表示[4] ただし複号は上が  , 下が
, 下が 
![{\displaystyle H_{\nu }^{(\iota )}(z)={\frac {\mp 2ie^{\mp \nu \pi i/2}}{\pi }}\int _{0}^{\infty }e^{\pm iz\cosh t}\cosh \nu t\,dt\ \ [|\mathrm {Re} (\nu )|<1,\pm \ \mathrm {Im} (z)>0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78d4f8e3c2a3471aa0c4228fde04dbf085f2ce26)
Whittaker の積分表示[5] ここに  はルジャンドル多項式
はルジャンドル多項式

漸近展開
 のときベッセル関数は以下の漸近形を持つ[6]。
のときベッセル関数は以下の漸近形を持つ[6]。








脚注
[脚注の使い方]
出典
- ^ “Bessel function”. Britannica. 2021年3月20日閲覧。
- ^ a b c 岩波数学公式, p. 178.
- ^ 岩波数学公式, p. 182.
- ^ a b 岩波数学公式, p. 183.
- ^ 岩波数学公式, p. 185.
- ^ 岩波数学公式, pp. 154, 168.
関連項目
- 特殊関数
- Jackson の q-Bessel 関数(英語版)
- Hahn-Exton の q-Bessel 関数(英語版)
参考文献
- Handbook of Mathematical Functions, Abramowitz and Stegun.
- Bessel Functions, Weisstein, Eric W. "Modified Bessel Functions" From MathWorld--A Wolfram Web Resource.
- A treatise on the theory of Bessel functions, George Neville Watson, Cambridge University Press,(1995).
- 森口繁一、宇田川銈久、一松信『岩波数学公式III 特殊函数』岩波書店、1987年。ISBN 4-00-005509-7。
外部リンク
- ベッセル関数の計算
- Bessel 関数の数値計算
- 古典的Bessel関数入門
典拠管理データベース: 国立図書館  | - フランス
- BnF data
- イスラエル
- アメリカ
- 日本
- チェコ
|
|---|
 第1種ベッセル関数
第1種ベッセル関数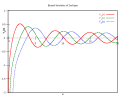 第2種ベッセル関数
第2種ベッセル関数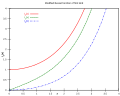 第1種変形ベッセル関数
第1種変形ベッセル関数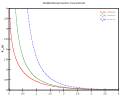 第2種変形ベッセル関数
第2種変形ベッセル関数




































![{\displaystyle {\frac {d^{2}y}{dx^{2}}}+{\frac {2}{x}}{\frac {dy}{dx}}+\left[1-{\frac {\alpha (\alpha +1)}{x^{2}}}\right]y=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dd52b8dbca43b9a94a4cdb7d2bebb90b56f7b9f)















![{\displaystyle {\frac {{\sqrt {\pi }}\Gamma (\nu +1/2)}{z^{\nu }}}H_{\nu }^{(\iota )}(z)=\mp 2^{\nu +1}i\int _{0}^{\pi /2}\exp \left\{\pm i\left[z-\left(\nu -{\frac {1}{2}}\right)\theta \right]-2z\cot \theta \right\}\,\cos ^{\nu -1/2}\theta \,\mathrm {cosec} ^{2\nu +1}\theta \,d\theta \ \ [\mathrm {Re} (\nu )>-{\frac {1}{2}},\ \mathrm {Re} (z)>0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9ff46890d9162f3ac92016f6f35258fcbe20c07)
![{\displaystyle H_{\nu }^{(\iota )}(z)={\frac {\mp 2ie^{\mp \nu \pi i/2}}{\pi }}\int _{0}^{\infty }e^{\pm iz\cosh t}\cosh \nu t\,dt\ \ [|\mathrm {Re} (\nu )|<1,\pm \ \mathrm {Im} (z)>0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78d4f8e3c2a3471aa0c4228fde04dbf085f2ce26)
















