解析学 において、ピカールの逐次近似法 (ピカールのちくじきんじほう、英 : Picard iteration )とは、常微分方程式 の初期値問題 に対し、解に一様収束 する関数列を構成する手法。常微分方程式の初期値問題と同値な積分方程式 に基づき、関数列を逐次的に構成する。常微分方程式の解の存在と一意性に関する基礎定理の証明に用いられる。より一般的な距離空間 論の観点からは、この逐次近似列の構成法は縮小写像 に対応しており、逐次近似法で得られる解は反復合成写像 の不動点 として捉えられる。ピカールの逐次近似法という名は19世紀のフランスの数学者エミール・ピカール に因む。ピカールは逐次近似の手法を発展させ、現在、常微分方程式の解の存在と一意性の理論で一般的に用いられる証明の論法を確立させた[7] [8]
導入 t を実数空間 R x t ) = (x 1 (t ), .., xm (t ))m -次実数空間 R m C m D を R m + 1R × C m f D 上で定義された R m C m
d d t x ( t ) = f ( t , x ( t ) ) {\displaystyle {\frac {d}{dt}}{\boldsymbol {x}}(t)={\boldsymbol {f}}(t,{\boldsymbol {x}}(t))} において、D 内の点 (τ , ξ に対し、初期条件
x ( τ ) = ξ {\displaystyle {\boldsymbol {x}}(\tau )={\boldsymbol {\xi }}} を満たす解 x t )τ を含む区間 I で求める初期値問題を考える。この初期値問題を解くことは積分方程式
x ( t ) = ξ + ∫ τ t f ( s , x ( s ) ) d s {\displaystyle {\boldsymbol {x}}(t)={\boldsymbol {\xi }}+\int _{\tau }^{t}{\boldsymbol {f}}(s,{\boldsymbol {x}}(s))\,ds} を解くことと同値である。
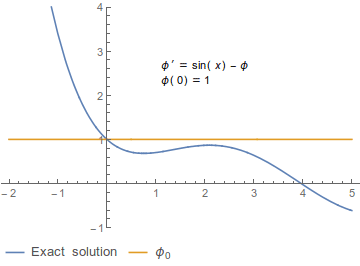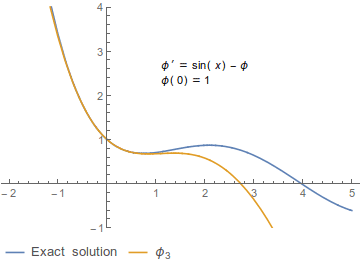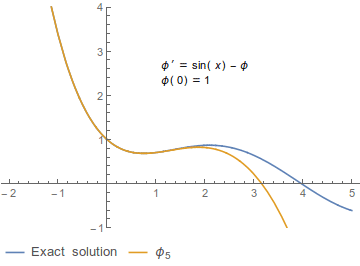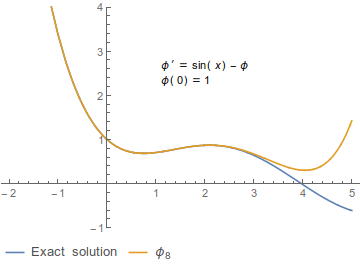
内容 ピカールの逐次近似法の例。非自励系の初期値問題 d / dt x (t ) = sin(t ) − x (t )x (0) = 1{φ n t )} である。ここで、φ 0 (t ) = 1φ 1 (t ) = 2 − cos(t ) − t φ 2 (t ) = 2 − cos(t ) − 2t + sin(t ) + t 2 /2 ピカールの逐次近似法では初期値問題と同値な積分方程式を基づき、次のように初期条件から逐次的に関数列 {φ n t )} を構成する[注 1]
φ 0 ( t ) = ξ , φ n ( t ) = ξ + ∫ τ t f ( s , φ n − 1 ( s ) ) d s ( n = 1 , 2 , ⋯ ) . {\displaystyle {\begin{aligned}{\boldsymbol {\varphi }}_{0}(t)&={\boldsymbol {\xi }},\\{\boldsymbol {\varphi }}_{n}(t)&={\boldsymbol {\xi }}+\int _{\tau }^{t}{\boldsymbol {f}}(s,{\boldsymbol {\varphi }}_{n-1}(s))\,ds\quad (n=1,2,\cdots ).\end{aligned}}} このとき、極限関数
φ ( t ) = lim n → ∞ φ n ( t ) {\displaystyle {\boldsymbol {\varphi }}(t)=\lim _{n\to \infty }{{\boldsymbol {\varphi }}_{n}(t)}} が存在すれば、これは上述の常微分方程式の初期値問題と同値な積分方程式を満たすことが期待される。
但し、この逐次近似法で構成する関数列 {φ n t )} が適切に定義され、その存在と収束が保証される必要がある。そのために次の条件を要請する。
R m + 1R × C m
E = { ( t , x ) : | t − τ | ≤ r , ‖ x − ξ ‖ ≤ ρ } {\displaystyle E=\{(t,{\boldsymbol {x}}):\,|t-\tau |\leq r,\,\|{\boldsymbol {x}}-{\boldsymbol {\xi }}\|\leq \rho \}} で f 有界 [注 2] M が存在して
‖ f ( t , x ) ‖ ≤ M {\displaystyle \|{\boldsymbol {f}}(t,{\boldsymbol {x}})\|\leq M} かつ、 x リプシッツ条件
‖ f ( t , x ) − f ( t , y ) ‖ ≤ L ‖ x − y ‖ {\displaystyle \|{\boldsymbol {f}}(t,{\boldsymbol {x}})-{\boldsymbol {f}}(t,{\boldsymbol {y}})\|\leq L\|{\boldsymbol {x}}-{\boldsymbol {y}}\|} を満たすとする[注 3]
r 0 := min ( r , ρ / M ) {\displaystyle r_{0}:=\min {(r,\rho /M)}} で定まる区間
I 0 = { t ∈ R : | t − τ | ≤ r 0 } {\displaystyle I_{0}=\{t\in \mathbb {R} :|t-\tau |\leq r_{0}\}} で {φ n t )} は
‖ φ n ( t ) − ξ ‖ ≤ ρ {\displaystyle \|{\boldsymbol {\varphi }}_{n}(t)-{\boldsymbol {\xi }}\|\leq \rho } を満たす連続関数として、適切に定義され、極限関数 φ t )φ n t )f φ t )
φ ( t ) = ξ + ∫ τ t f ( s , φ ( s ) ) d s {\displaystyle {\boldsymbol {\varphi }}(t)={\boldsymbol {\xi }}+\int _{\tau }^{t}{\boldsymbol {f}}(s,{\boldsymbol {\varphi }}(s))\,ds} を満たし、所与の常微分方程式の初期値問題の解である。
縮小写像の不動点定理 積分作用素 T を
T ϕ = ξ + ∫ τ t f ( s , ϕ ( s ) ) d s {\displaystyle T{\boldsymbol {\phi }}={\boldsymbol {\xi }}+\int _{\tau }^{t}{\boldsymbol {f}}(s,{\boldsymbol {\phi }}(s))\,ds} で定めると、上述の積分方程式の解は、
T ϕ = ϕ {\displaystyle T{\boldsymbol {\phi }}={\boldsymbol {\phi }}} を満たす T の不動点 である。ピカールの逐次近似法では、関数列 {φ n t )} は T の反復合成
T φ n = φ n − 1 {\displaystyle T{\boldsymbol {\varphi }}_{n}={\boldsymbol {\varphi }}_{n-1}} で構成されるが、一定の条件の下では T は縮小写像 となり、不動点定理 からも解の存在が保証される。 実際、先ほどと同様に、f E で連続かつリプシッツ連続であるとする。ここで
0 < L r 0 ′ < 1 , r 0 ′ ≤ r 0 {\displaystyle 0<Lr_{0}'<1,\quad r_{0}'\leq r_{0}} を満たす正の定数 r 0 ′
I 0 ′ = { t ∈ R : | t − τ | ≤ r 0 ′ } {\displaystyle I_{0}'=\{t\in \mathbb {R} :|t-\tau |\leq r_{0}'\}} をとる。I 0 ′R m C m C {\displaystyle {\mathcal {C}}} C {\displaystyle {\mathcal {C}}} ノルム を
‖ ϕ ‖ I 0 ′ = max t ∈ I 0 ′ ‖ ϕ ( t ) ‖ {\displaystyle \|{\boldsymbol {\phi }}\|_{I_{0}'}=\max _{t\in I_{0}'}\|{\boldsymbol {\phi }}(t)\|} で定めると、 C {\displaystyle {\mathcal {C}}} 完備 なノルム空間 となる。 C {\displaystyle {\mathcal {C}}}
‖ ϕ ( t ) − ξ ‖ ≤ ρ {\displaystyle \|{\boldsymbol {\phi }}(t)-{\boldsymbol {\xi }}\|\leq \rho } を満たすものからなる F {\displaystyle {\mathcal {F}}} T は F {\displaystyle {\mathcal {F}}} F {\displaystyle {\mathcal {F}}}
‖ T ϕ − T ψ ‖ I 0 ′ ≤ L r 0 ′ ‖ ϕ − ψ ‖ I 0 ′ ( ϕ , ψ ∈ F ) {\displaystyle \|T{\boldsymbol {\phi }}-T{\boldsymbol {\psi }}\|_{I_{0}'}\leq Lr_{0}'\|{\boldsymbol {\phi }}-{\boldsymbol {\psi }}\|_{I_{0}'}\quad ({\boldsymbol {\phi }},\,{\boldsymbol {\psi }}\in {\mathcal {F}})} を満たす縮小写像である。よって、バナッハの不動点定理 により、Tφ = φ F {\displaystyle {\mathcal {F}}} I 0 ′φ t )[注 4]
例 例1 次の自励系 のスカラー微分方程式の初期値問題を考える。
d x ( t ) d t = x ( t ) , x ( 0 ) = 1. {\displaystyle {\frac {dx(t)}{dt}}=x(t),\quad x(0)=1.} ピカールの逐次近似法で φn (t )
φ 1 ( t ) = 1 + ∫ 0 t 1 d s = 1 + t , φ 2 ( t ) = 1 + ∫ 0 t ( 1 + s ) d s = 1 + t + t 2 2 , ⋮ φ n ( t ) = 1 + t + t 2 2 + ⋯ + t n n ! = ∑ l = 0 n t l l ! . {\displaystyle {\begin{aligned}\varphi _{1}(t)&=1+\int _{0}^{t}1\,ds=1+t,\\\varphi _{2}(t)&=1+\int _{0}^{t}(1+s)\,ds=1+t+{\frac {t^{2}}{2}},\\&\vdots \\\varphi _{n}(t)&=1+t+{\frac {t^{2}}{2}}+\cdots +{\frac {t^{n}}{n!}}=\sum _{l=0}^{n}{\frac {t^{l}}{l!}}.\end{aligned}}} よって、解は
φ ( t ) = lim n → ∞ φ n ( t ) = e t {\displaystyle \varphi (t)=\lim _{n\to \infty }{\varphi _{n}(t)}=e^{t}} となる。
例2 次のスカラー微分方程式の初期値問題を考える。
d x ( t ) d t = t x ( t ) , x ( 0 ) = 1 {\displaystyle {\frac {dx(t)}{dt}}=tx(t),\quad x(0)=1} ピカールの逐次近似法で φn (t )
φ 1 ( t ) = 1 + ∫ 0 t s d s = 1 + t 2 2 φ 2 ( t ) = 1 + ∫ 0 t s ( 1 + s 2 2 ) d s = 1 + t 2 2 + t 4 2 ⋅ 4 ⋯ φ n ( t ) = 1 + t 2 2 + t 4 2 ⋅ 4 + ⋯ + t 2 n 2 ⋅ 4 ⋯ ⋅ ( 2 n ) = ∑ l = 0 n 1 l ! ( t 2 2 ) l {\displaystyle {\begin{aligned}\varphi _{1}(t)&=1+\int _{0}^{t}s\,ds=1+{\frac {t^{2}}{2}}\\\varphi _{2}(t)&=1+\int _{0}^{t}s\left(1+{\frac {s^{2}}{2}}\right)ds=1+{\frac {t^{2}}{2}}+{\frac {t^{4}}{2\cdot 4}}\\&\cdots \\\varphi _{n}(t)&=1+{\frac {t^{2}}{2}}+{\frac {t^{4}}{2\cdot 4}}+\cdots +{\frac {t^{2n}}{2\cdot 4\cdots \cdot (2n)}}=\sum _{l=0}^{n}{\frac {1}{l!}}\left({\frac {t^{2}}{2}}\right)^{l}\end{aligned}}} よって、解は
φ ( t ) = lim n → ∞ φ n ( t ) = e t 2 / 2 {\displaystyle \varphi (t)=\lim _{n\to \infty }{\varphi _{n}(t)}=e^{t^{2}/2}} となる。
リプシッツ条件についての注意 リプシッツ条件が満たされない場合、逐次近似列 {φ n t )} が定義されても、その収束は保証されない。そのような場合として、次の例を考える。
D = { ( t , x ) ∈ R 2 : − ∞ < t < 1 , − ∞ < x < ∞ } {\displaystyle D=\{(t,x)\in \mathbb {R} ^{2}:-\infty <t<1,\,-\infty <x<\infty \}} とし、f (t , x )
f ( t , x ) = { 0 ( − ∞ < t ≤ 0 , x ∈ R ) 2 t ( 0 < t ≤ 1 , − ∞ < x < 0 ) 2 t − 4 x t ( 0 < t ≤ 1 , 0 ≤ x ≤ t 2 ) − 2 t ( 0 < t ≤ 1 , t 2 < x < ∞ ) {\displaystyle f(t,x)={\begin{cases}0&\quad (-\infty <t\leq 0,\,x\in \mathbb {R} )\\2t&\quad (0<t\leq 1,\,-\infty <x<0)\\2t-{\frac {4x}{t}}&\quad (0<t\leq 1,\,0\leq x\leq t^{2})\\-2t&\quad (0<t\leq 1,\,t^{2}<x<\infty )\end{cases}}} で定義すると、D 上で f (t , x )
| f ( t , x ) | ≤ 2 ( ( t , x ) ∈ D ) {\displaystyle |f(t,x)|\leq 2\quad ((t,x)\in D)} で有界であるが、リプシッツ連続ではない。このとき、初期値問題
d x ( t ) d t = f ( t , x ) , x ( 0 ) = 0 {\displaystyle {\frac {dx(t)}{dt}}=f(t,x),\quad x(0)=0} を考えると、逐次近似列は
φ 2 k − 1 ( t ) = t 2 , φ 2 k ( t ) = − t 2 ( k = 1 , 2 , ⋯ ) {\displaystyle \varphi _{2k-1}(t)=t^{2},\,\varphi _{2k}(t)=-t^{2}\quad (k=1,2,\cdots )} となり、収束しない。一方で、解は
φ ( t ) = t 3 3 {\displaystyle \varphi (t)={\frac {t^{3}}{3}}} である。
脚注 [脚注の使い方 ]
注釈 ^ φ 0 (t )‖ φ 0 (t ) − ξ ρ を満たす任意の連続関数でよい。^ 有界閉領域上の連続関数であるから、有界性定理 により、有界性が保証される。 ^ リプシッツ条件の下では解の一意性が保証される。なお、 {φ n t )} が適切に定義されるにはリプシッツ条件は不要だが、その場合、収束は保証されない。 ^ ここでの議論では、T が縮小写像の条件を満たすように制約条件 0 < Lr ′ < 1 を加えたため、解の存在が保証される区間は当初の I 0 = [τ − r 0 , τ + r 0 ]I 0 ′ = [τ − r 0 ′, τ + r 0 ′]I 0 m をとると Tm を縮小写像とすることができるため、不動点定理を用いて I 0 出典 参考文献 木村, 俊房 『常微分方程式』共立出版 〈共立数学講座13〉、1974年11月。ISBN 978-4-320-01104-5。 NCID BN01224519。全国書誌番号 :69007185。http://www.kyoritsu-pub.co.jp/bookdetail/9784320011045 。 山本, 稔『常微分方程式の安定性』実教出版 〈実教理工学全書〉、1979年1月。ISBN 978-4407022032。 NCID BN0039709X。全国書誌番号 :79032265。 吉田, 耕作 『微分方程式の解法』(第2版)岩波書店 〈岩波全書 〉、1978年2月23日。ISBN 978-4000215541。 NCID BN00692555。全国書誌番号 :78010853。 A. N. Kolmogorov & A. P. Yushkevich 編 編、藤田宏 監 訳『19世紀の数学III チェビシェフの関数論・常微分方程式・変分法・差分法』朝倉書店 、2009年11月。ISBN 978-4254117431。 NCID BB00312489。OCLC 675973814。全国書誌番号 :21686817。 Hartman, Philip (1964). Ordinary Differential Equations . John Wiley & Sons Kolmogorov, Andrey ; Fomin, Sergei V. Richard A. Silverman訳 (June 1, 1975) [1970]. Introductory Real Analysis . Dover Books on Mathematics (Revised English ed.). New York : Dover Press . ISBN 0-486-61226-0. NCID BA03478607. LCCN 74-18669. OCLC 468055856 関連項目