Martingala (matematica)

Questa voce sull'argomento teoria della probabilità è solo un abbozzo.

Contribuisci a migliorarla secondo le convenzioni di Wikipedia.

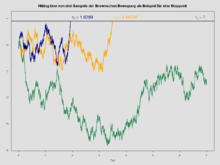
Nella teoria della probabilità, una martingala è un processo stocastico ${\displaystyle X_{t}}$, indicizzato da un parametro crescente ${\displaystyle t}$ (spesso interpretabile come tempo), con la seguente proprietà: per ogni ${\displaystyle s\leq t}$, l'attesa di ${\displaystyle X_{t}}$ condizionata rispetto ai valori di ${\displaystyle X_{r},r\leq s}$, è uguale ad ${\displaystyle X_{s}}$. Il più noto esempio di martingala, in cui il parametro ${\displaystyle s}$ è continuo, è senz'altro il moto browniano.

Prima di dare una definizione precisa, illustriamo un esempio. Consideriamo un uomo che giochi a testa o croce con una moneta: ad ogni lancio della moneta guadagna un euro nel caso esca testa, mentre perde un euro in caso esca croce. Sia ${\displaystyle X_{0},X_{1},X_{2},\ldots }$ il denaro (espresso in euro) posseduto dall'uomo rispettivamente prima del primo lancio (${\displaystyle X_{0}}$), dopo il primo lancio (${\displaystyle X_{1}}$), dopo il secondo lancio (${\displaystyle X_{2}}$) e così via.

Se la moneta non è truccata (cioè se le probabilità di vincere e perdere ad ogni lancio sono uguali), il valore atteso di ${\displaystyle X_{n}}$, ovvero del denaro posseduto dopo ${\displaystyle n}$ lanci, sarà semplicemente ${\displaystyle X_{0}}$, ovvero il numero di euro inizialmente posseduti. Ma se veniamo a sapere che dopo ${\displaystyle m}$ lanci questo signore possiede ${\displaystyle {\bar {x}}}$ €, l'aspettativa più ragionevole riguardo agli euro guadagnati dopo ${\displaystyle n}$ lanci (con ${\displaystyle n>m}$) sarà invece ${\displaystyle {\bar {x}}}$. Questa è appunto la proprietà di martingala.

In ambito matematico, il termine martingala si riferiva originariamente ad una serie di strategie utilizzate dagli scommettitori francesi nel XVIII secolo. La più semplice di queste strategie veniva utilizzata in giochi simili all'odierno testa o croce: lo scommettitore sceglieva una faccia di una moneta. Questa veniva lanciata, ed il giocatore guadagnava o perdeva una quantità prefissata di denaro a seconda che avesse indovinato o meno la faccia mostrata dalla moneta dopo la caduta. La strategia della martingala consisteva nel raddoppiare la puntata dopo ogni lancio perso. Questa tecnica, che apparentemente conduce ad una vincita finale certa, è stata in verità la causa di forti perdite da parte di scommettitori. Un'analisi più attenta mostra che la posta da mettere in gioco aumenta esponenzialmente con i lanci perdenti, e ci si convince facilmente del fatto che, per assicurarsi la vittoria, bisognerebbe disporre di un capitale infinito da poter scommettere, e bisognerebbe che anche il banco fosse disposto ad accettare poste di qualsiasi taglia. La vincita netta è solamente la posta iniziale. Ironia della sorte, uno dei risultati elementari dimostrati dall'odierna teoria delle martingale è proprio l'inesistenza di un sistema di scommesse vincente.

Il concetto di martingala è stato introdotto nella teoria della probabilità da Paul Pierre Lévy. Gran parte dei risultati avanzati riguardanti le martingale sono stati prodotti da Joseph Leo Doob, con contributi importanti da parte di Kiyoshi Itō sulle applicazioni analitiche. Dagli anni settanta, la teoria delle martingale ha trovato ampie applicazioni in molti settori della matematica pura ed applicata. In particolare, nella teoria della probabilità, in fisica matematica, ed in finanza matematica. Il successo di tale teoria è tale che essa risulta una delle poche branche della matematica nota anche a studiosi di altre discipline, in particolare da chi si occupa di finanza e tecniche di borsa. Anche grazie ai contributi dati a questa teoria, Lévy, Itō e Doob sono considerati tra i maggiori matematici del XX secolo.

Una martingala a tempo discreto è un processo stocastico a tempo discreto ${\displaystyle X_{1},\ldots ,X_{n},\ldots }$ a valori in ${\displaystyle \mathbb {R} }$ tale che

${\displaystyle \mathbf {E} (\vert X_{n}\vert )<\infty ,}$

${\displaystyle \mathbf {E} (X_{n+1}|X_{1}\dots X_{n})=X_{n},\quad n\in \mathbb {N} .}$

Un processo stocastico ${\displaystyle X_{t},t\geq 0}$ è una martingala se

${\displaystyle \mathbf {E} (\vert X_{t}\vert )<\infty ,}$

${\displaystyle \mathbf {E} (X_{t}|\{X_{u}\}_{u\leq s})=X_{s},\quad \forall \ s\leq t,}$

Più in generale, un processo stocastico ${\displaystyle Y:T\times \Omega \rightarrow S}$ si dice martingala rispetto ad una filtrazione ${\displaystyle {\mathcal {F}}}$ ed una misura di probabilità ${\displaystyle \mathbb {P} }$ se:

• ${\displaystyle {\mathcal {F}}}$ è una filtrazione dello spazio di probabilità ${\displaystyle (\Omega ,\Sigma ,\mathbb {P} )}$ che stiamo studiando
• ${\displaystyle Y}$ è adattato alla filtrazione, ovvero per ogni ${\displaystyle t\in T}$ la variabile aleatoria ${\displaystyle Y_{t}}$ è misurabile secondo ${\displaystyle {\mathcal {F}}_{t}}$
• ${\displaystyle \mathbf {E} _{P}(\vert Y_{t}\vert )<\infty \quad \forall t}$
• ${\displaystyle \mathbf {E} _{P}([Y_{t}-Y_{s}]\chi _{F})=0\quad \forall s,t:s<t,\ \forall F\in {\mathcal {F}}_{s}}$

Il processo stocastico ${\displaystyle (X_{n})_{n\in \mathbb {R} _{+}}}$è una submartingala (o sottomartingala) se valgono i primi quattro punti della definizione di martingala e la previsione condizionale di ${\displaystyle X_{t}}$, sapendo i valori contenuti nella filtrazione ${\displaystyle {\mathcal {F}}}$ è maggiore o uguale a ${\displaystyle X_{s}}$, per ogni ${\displaystyle s<t}$, ossia

${\displaystyle \mathbf {E} _{P}([Y_{t}]\chi _{F})\geqslant Y_{s}\quad \forall s,t:s<t,\ \forall F\in {\mathcal {F}}_{s}}$

Il processo stocastico ${\displaystyle (X_{n})_{n\in \mathbb {R} _{+}}}$è una supermartingala se valgono i primi quattro punti della definizione di martingala e la previsione condizionale di ${\displaystyle X_{t}}$, sapendo i valori contenuti nella filtrazione ${\displaystyle {\mathcal {F}}}$ è minore o uguale a ${\displaystyle X_{s}}$, per ogni ${\displaystyle s<t}$, ossia

${\displaystyle \mathbf {E} _{P}([Y_{t}]\chi _{F})\leqslant Y_{s}\quad \forall s,t:s<t,\ \forall F\in {\mathcal {F}}_{s}}$

Si consideri un'urna contenente inizialmente due palline, una bianca e una nera. Ad ogni estrazione si pesca dall'urna una pallina, si verifica il colore e quindi la si reintroduce nell'urna assieme ad un'altra pallina dello stesso colore. Ad esempio, se alla prima estrazione si pesca una pallina nera, viene inserita nell'urna la pallina appena pescata e un'altra pallina nera. Nella seconda estrazione, quindi, ci saranno due palline nere e una bianca.

Sia ${\displaystyle (Y_{n})_{n\geqslant 0}}$ un processo stocastico che conta il numero di palline nere ad ogni istante ${\displaystyle n,\forall {n\geqslant 0}}$. Si pone ${\displaystyle X_{n}={\dfrac {Y_{n}}{n+2}}}$ la proporzione di palline nere all'istante ${\displaystyle n}$. Si noti che al primo istante, quando ${\displaystyle n=0}$, ci sono due palline nell'urna, una nera e una bianca. Si definisce ${\displaystyle U_{k}=\mathrm {I} _{\{{\text{estraggo pallina nera all'istante }}k\}}}$la funzione indicatrice dell'estrazione di una pallina nera all'istante ${\displaystyle k}$. La ${\displaystyle \sigma }$-algebra generata da ${\displaystyle (U_{1},\ldots ,U_{k})}$ è una filtrazione ${\displaystyle {\mathcal {F}}^{U}=({\mathcal {F}}_{i}^{U})_{i\geqslant 1}}$ dello spazio ${\displaystyle (\Omega ,{\mathcal {A}},P)}$.

La previsione del numero di palline nere all'istante ${\displaystyle n+1}$ sapendo il numero di palline nere estratte all'istante ${\displaystyle n}$ è ${\displaystyle E[Y_{n+1}|{\mathcal {F}}_{n}^{U}]={\dfrac {n+3}{n+2}}Y_{n}}$. La previsione della proporzione di palline nere presenti nell'urna all'istante ${\displaystyle n+1}$ è ${\displaystyle E[X_{n+1}|{\mathcal {F}}_{n}^{U}]=E{\biggl [}{\dfrac {Y_{n+1}}{n+3}}|{\mathcal {F}}_{n}^{U}{\biggr ]}={\dfrac {1}{n+3}}E[Y_{n+1}|{\mathcal {F}}_{n}^{U}]={\dfrac {Y_{n}}{n+2}}=X_{n}}$.

Poiché risulta ${\displaystyle E[X_{n+1}|{\mathcal {F}}_{n}^{U}]=X_{n}}$, si può concludere che ${\displaystyle (X_{n})_{n\geqslant 0}}$ è una martingala rispetto a ${\displaystyle {\mathcal {F}}^{U}}$.

• (EN) Daniel Revuz e Marc Yor, Continuous Martingales and Brownian motion, 3ª ed., Heidelberg, Springer, 1999, ISBN 3-540-64325-7. URL consultato il 21 novembre 2021.

• Differenza di martingala
• Teorema di arresto opzionale di Doob
• Semimartingala

• (EN) martingale, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Martingala, su MathWorld, Wolfram Research.
• Home page di Srinivasa Ravi Varadhan, con del materiale introduttivo alla teoria delle martingale.

V · D · M Probabilità
Teoria della probabilità	Evento · Spazio campionario · Indipendenza stocastica · Probabilità condizionata · Teorema di Bayes · Disuguaglianza di Čebyšëv · Disuguaglianza di Markov
Variabili casuali	Misura di probabilità · Funzione di densità di probabilità · Funzione di ripartizione · Funzione caratteristica · Funzione generatrice dei momenti · Convergenza di variabili casuali
Distribuzioni di probabilità univariate	Distribuzioni discrete Uniforme discreta · Binomiale (Bernoulliana) · Degenere · Ipergeometrica · Di Pascal · Geometrica · Poissoniana Distribuzioni continue Uniforme continua · Normale · Esponenziale · Beta · Gamma · t di Student · di Cauchy · Chi Quadrato
Distribuzioni di probabilità multivariate	Multinomiale · Normale multivariata · Wishart · Dirichlet
Processi stocastici	Matrice stocastica · Processo markoviano · Passeggiata aleatoria · Martingala · Moto browniano · Integrale di Itō · Equazione differenziale stocastica
Discipline connesse	Combinatoria · Statistica

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica