Bénéfice de synergie


Cet article ne cite aucune source et peut contenir des informations erronées (signalé en avril 2023).
Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».
- Archive Wikiwix
- Bing
- Cairn
- DuckDuckGo
- E. Universalis
- Gallica
- G. Books
- G. News
- G. Scholar
- Persée
- Qwant
- (zh) Baidu
- (ru) Yandex
- (wd) trouver des œuvres sur Wikidata
En microéconomie, le bénéfice de synergie est un avantage global supplémentaire découlant de la décision d’un ensemble d’acteurs de mettre en commun des ressources ou des moyens, de coordonner des actions en visant une même finalité.
Les acteurs peuvent être des secteurs d’activité d’une même entreprise (utilisant des ressources communes), ou des entités économiquement distinctes qui s’organisent au sein d’un partenariat fondé sur des règles admises par tous.
Lorsque les acteurs souhaitent préserver leur indépendance économique, ils sont confrontés à devoir gérer une complexité accrue, contraints de définir et d’accepter les modalités de leur collaboration. Les principaux problèmes concernent la caractérisation quantitative du bénéfice de synergie et la manière de le répartir entre les acteurs : mal résolus, ces problèmes induisent une instabilité de l’alliance qui conduit naturellement à son éclatement.
Fusion d’entreprises
Toute opération de fusion-acquisition d’entreprises ou de rachat de concurrents permet d’engendrer un bénéfice de synergie :
- par l’augmentation des compétences internes,
- par une utilisation plus rationnelle des ressources,
- par la réorganisation des activités (il est possible de faire mieux après qu’avant),
- par les économies d'échelle et la diminution des coûts de production,
- par l’amélioration de la position sur les marchés,
- etc.
En théorie, la fusion est l’approche la plus simple dans le sens où elle élude la question délicate de la répartition du bénéfice de synergie entre les acteurs puisqu’en fin de compte il n’en reste qu’un.
Les cartels et les ententes illicites exploitent également une source de synergie qui se réalise entièrement aux dépens d’autres acteurs, c'est-à-dire les clients.
Achats groupés
Plusieurs petits consommateurs d’un même type de produit groupent leurs demandes individuelles afin de présenter au marché une demande résultante. Par exemple :
- Combustible de chauffage : en passant une commande unique, divers propriétaires localisés dans un même quartier obtiennent un prix plus intéressant (rabais de quantité).
- Produits financiers : divers petits épargnants placent leurs actifs financiers dans un fonds de placement leur permettant d’acquérir ensemble un portefeuille plus richement diversifié, une réduction des coûts de transaction et une gestion centralisée des risques.
Définition de la stabilité d’une répartition
Pour caractériser un mode de répartition du bénéfice de synergie obtenu au sein de l’alliance d’un ensemble d’acteurs, un critère de stabilité peut être formulé de la manière suivante :
Définition — Un mode de répartition est stable si aucun sous-groupe d’acteurs n’est économiquement incité à se séparer de l’ensemble.
Ce critère est satisfait lorsque, pour tout sous-groupe donné, le bénéfice de synergie global issu des seuls membres du sous-groupe n’est pas supérieur à la somme des bénéfices que ses membres obtiendraient en restant au sein de l’alliance initiale. La stabilité ainsi définie s’apparente à un optimum de Pareto local. Cependant, l’alliance est menacée dès l’existence d’un sous-groupe particulier ne satisfaisant pas cette propriété.
En particulier, pour qu’un tel mode de répartition existe, il est nécessaire que le bénéfice de synergie total n’augmente pas lorsqu’un acteur quitte l’alliance. Cette condition n’implique cependant pas que la contribution spécifique d’un acteur donné soit nécessairement favorable à chacun des autres.
Répartition d’une ressource limitée
Un ensemble de partenaires se partagent une ressource quantitativement limitée conformément à leurs parts respectives qui sont supposées être légalement établies. Par exemple :
- Un ensemble de surfaces agricoles appartenant respectivement à des propriétaires éleveurs de bétail.
- Une ressource en eau qui est répartie en parts prédéfinies entre des sociétés indépendantes assurant respectivement la consommation publique, l’irrigation et la production hydroélectrique.
D’un commun accord et dans un esprit de collaboration, les partenaires peuvent décider de modifier temporairement les parts légales dans le but de retirer un revenu globalement supérieur à celui dont ils bénéficieraient autrement : cet accroissement de revenu est le bénéfice de synergie de l’ensemble.
Bien que l’incidence économique des nouvelles parts momentanément attribuées soit favorable à l’ensemble, ce ne sera sans doute pas le cas pour chacun ; il est donc essentiel d’établir de règles précises de compensation des revenus individuels afin que chacun retrouve finalement un intérêt tangible dans l’opération : ces règles doivent permettre à chaque partenaire de bénéficier au minimum du revenu qu’il obtiendrait hors alliance, auquel s’ajoutera une part du bénéfice de synergie qui soit en rapport avec sa propre contribution à ce dernier.
Mode de répartition stable
Considérons acteurs se partageant une ressource limitée. Supposons que chacun d’eux soit en mesure d’élaborer une fonction décrivant l’avantage (on parlera ici de revenu) que leur procurerait une part (variable) de la ressource dont il disposerait en propre au sein d’une alliance, ceci durant une période limitée et la même pour tous. Supposons également que chaque acteur valide l’objectivité des fonctions des autres.
Propriétés naturelles des fonctions de revenu :
- Chaque % de ressource supplémentaire accordée à un acteur lui apporte généralement une augmentation de son revenu : c’est une propriété de croissance de la fonction. Il est possible, bien que ce soit peu fréquent, qu’à partir d’une quantité de ressource très élevée, la fonction se mette à décroître : « trop c’est trop » et l’acteur doit payer pour détruire un excédent de ressource dont il ne sait plus que faire.
- À chaque % de ressource supplémentaire accordée à un acteur, l’augmentation de son revenu s’atténue au fur et à mesure que sa part augmente : c’est une propriété de concavité de la fonction (l’allure de la fonction a la forme d’un « bol renversé » : tout segment dont les extrémités se situent sur le graphe se trouve intégralement « au-dessous » du graphe).
Considérons les notations et hypothèses suivantes :
- est la part contractuelle de l’acteur comprise entre 0 et 1,
- indique que la totalité de la ressource est distribuée,
- désigne la fonction de revenu dépendant de la part (inconnue comprise entre 0 et 1),
- est le profit de l’acteur découlant de sa part contractuelle.
La maximisation du profit total s’obtient en résolvant le problème suivant :
- Trouver les inconnues satisfaisant qui maximisent
- sous la contrainte
- .
Puisque les parts contractuelles sont des candidats admissibles, le profit total obtenu indépendamment par les acteurs est inférieur ou égal au profit maximal , valeur définie comme le maximum des sous respect des contraintes.
Le bénéfice global de synergie est alors la différence .
L’hypothèse de concavité des fonctions permet d’assurer que ce problème admet toujours une solution et qu’il existe des méthodes simples et robustes permettant de la déterminer numériquement.
Existence d’une solution :
Les fonctions de la variable scalaire étant concaves, elles sont continues, tout comme la fonction définie sur le domaine qui est caractérisé par les contraintes. étant un espace fermé et compact, le théorème des bornes implique l’existence dans d’un point qui maximise .
Caractéristiques d’une solution :
En introduisant un multiplicateur de Lagrange , c'est-à-dire une variable supplémentaire, le problème de recherche du maximum peut se formuler de la manière suivante :
- Trouver le scalaire et les qui maximisent
- .
correspond au revenu marginal de l’ensemble des acteurs par rapport à la quantité (relative) de ressource totale disponible.
Méthode de recherche d’une solution :
La concavité des implique qu’elles sont dérivables, hormis en certains points (dont le nombre est au plus dénombrable) sur lesquels des dérivées « à gauche » et « à droite » existent.
Pour simplifier, faisons abstraction de ces points de singularité. Les sont donc provisoirement supposées dérivables et ces dérivées sont décroissantes.
On peut finalement formuler le problème de la manière suivante :
- Trouver auquel on associe les définis par
- si ,
- si ,
- si ,
- satisfaisant .
Si les points de singularité des dérivées existent, avec les dérivées à gauche (g) et à droite (d), la première condition s’écrit
- si .
Sous cette forme, il est facile de résoudre le problème en appliquant par exemple une méthode de bissection sur jusqu’à satisfaire la dernière contrainte. En effet, si augmente, les (définis par les 3 conditions qui les caractérisent) diminuent et réciproquement.
Autre propriété :
Par construction, la droite de pente passant par le point est une tangente à la courbe en ce point. Par concavité, cette droite se situe « au-dessus » du graphe de la fonction.
En particulier, il existe un scalaire (multiplicateur de Lagrange de la contrainte ) correspondant au revenu marginal de l’ensemble des acteurs par rapport à la quantité de ressource totale disponible (s’il était possible d’augmenter la ressource totale de 1 %, alors le revenu total de l’alliance augmenterait d’environ ).
Le mode de répartition suivant est stable au sens de la définition qui est donnée plus haut :
- Au lieu d’exploiter sa part contractuelle , l’acteur se voit attribuer la part qui est la solution du problème précédent. À ce stade, la totalité de la ressource disponible est bien répartie entre les acteurs.
- Afin de compenser l’écart de part de l’acteur , il échange avec un « pot commun » le montant qui doit être versé si ou retiré du pot si .
- Puisque , la somme algébrique des échanges avec le pot commun est nulle.
Avec ce mode de répartition, le profit de l’acteur atteint en fin de compte le montant
On vérifie que ce nouveau profit ne peut pas être inférieur au profit obtenu hors alliance avec la part contractuelle. Graphiquement, la droite de pente passant par le point est une tangente à la courbe en ce point. Par concavité, cette tangente est située « au-dessus » du graphe de la fonction.
Le bénéfice de synergie qui revient en propre à l’acteur , (c'est-à-dire son intérêt économique à participer à l’alliance) est alors la différence d’ordonnées entre la tangente et la fonction calculée à l’abscisse .
Soit un sous-groupe d’acteurs et les parts respectives conduisant au profit maximal que ces seuls acteurs peuvent obtenir en mettant en commun leurs parts contractuelles. Ainsi
- .
D’autre part, en reprenant la solution de l’ensemble des acteurs, la tangente étant située « au-dessus » de la fonction, il en découle
En sommant cette relation sur dans , il vient
Cette inégalité indique justement que le profit maximal que le sous-groupe peut obtenir à l’interne (membre de gauche) n’excède pas la somme des profits individuels que ses membres obtiendraient au sein de l’alliance globale (membre de droite).
Synergie de financements
Tel que décrit ci-dessus, le mode de répartition d’une ressource limitée s’applique à d’autres domaines, en particulier celui de l’emprunt et du financement.
Il est économiquement naturel que, plus le montant emprunté par un acteur augmente (toute chose étant égale par ailleurs), plus le coût (ou le taux d’intérêt) augmente. Au niveau de l’entreprise, le rendement espéré des obligations reste inférieur à celui des actions, la raison sous-jacente étant la nature différente des risques en cas de défaut de l’émetteur.
En d’autres termes, chaque tranche d’emprunt supplémentaire devrait théoriquement coûter un peu plus cher que les tranches précédentes : le taux marginal est croissant. Ainsi, la fonction qui, à un montant total emprunté par un acteur, associe le coût (annuel) satisfait une propriété de convexité.
Sur la base de ce constat, plusieurs acteurs peuvent envisager un partenariat au sein duquel les emprunts sont centralisés, ceci afin de réaliser un bénéfice de synergie sur le coût total du capital. Le mécanisme d’une répartition stable de ce bénéfice est en tout point semblable à celui développé ci-dessus : il suffit de changer le signe de la fonction convexe de coût du capital pour obtenir une fonction concave de profit.
Une telle approche se différencie très significativement d’une simple mutualisation des dettes respectives et des risques associés : en effet, chaque acteur trouvera un avantage réel au sein du partenariat et ne sera surtout pas contraint de se financer aux conditions moyennes de l’ensemble (ce qui serait à l’évidence une approche totalement instable).
Application aux dettes nationales des membres de l’UE
Au sein de l’UE, les mêmes considérations permettent d’affirmer que la somme des coûts des dettes nationales (contractées isolément) excède le coût de la dette totale acquise de manière centralisée par la BCE au nom de ses membres.
Il y aurait ainsi un intérêt tangible à mettre en œuvre un tel mécanisme car il apporte une contribution significative à la résolution du problème de la crise de la dette. Ne pas exploiter ce bénéfice de synergie revient simplement à prélever ce même montant des fonds publics pour en faire cadeau aux marchés financiers.
Dans ce contexte, les bases d’un partenariat consistent à :
- substituer les dettes nationales par des Euro-obligations,
- évaluer consensuellement chacun des coûts spécifiques des dettes nationales (taux moyens estimés des emprunts en fonction du montant de la dette),
- quantifier le bénéfice de synergie ainsi dégagé,
- le répartir entre tous les membres de manière « appropriée ».
En pratique, chaque membre de l’UE élabore en accord avec les autres une courbe caractérisant le plus objectivement possible le coût annuel d’une dette qui, à ce stade, reste un paramètre. Ces fonctions tiennent compte de nombreuses spécificités propres (tels le PIB, la capacité de l’état à couvrir ses dépenses et les mesures prises pour y parvenir, les taux de chômage et de croissance, les fonds publics du patrimoine, etc). Bien que la tâche ne soit pas aisée, il est sans doute plus facile de trouver un compromis sur les profils de ces courbes que de convaincre les « bons élèves » à payer pour les autres.
Partant de ces fonctions et des dettes effectives , il s’agit de résoudre le problème suivant :
- Trouver les inconnues qui minimisent
- sous la contrainte
- .
En particulier, la solution permet d’évaluer le scalaire (multiplicateur de Lagrange de la contrainte) correspondant au coût marginal de la fonction objectif par rapport au membre de droite de la contrainte. permet finalement de déterminer le coût total à payer par chacun des membres pour le financement de sa propre dette, soit
(dont la somme atteint l’optimum de la fonction objectif .
Si les fonctions correspondent à la perception des marchés, le montant devrait correspondre au coût effectif du financement total. S’il subsiste un écart, il convient d’adapter « uniformément » les fonctions des membres afin de résorber la différence.
Dans ce mécanisme, chaque membre perçoit un avantage d’autant plus élevé que le coût marginal de sa propre dette s’écarte du coût marginal de l’ensemble. Les seuls qui ne retirent qu’un faible avantage sont ceux dont la dette effective reste proche de la dette de la solution (). Le bénéfice de synergie est alors principalement distribué entre les membres qui y contribuent, c'est-à-dire les « bons » et aux « mauvais » élèves.
Les résultats présentés ici constituent une simple illustration numérique du mécanisme à l’aide de données issues des publications de l’OCDE (année 2011 pour le taux d’endettement et année 2010 pour le PIB, taux de change admis 0.707 €/US$).
Les fonctions envisagées ici sont particulièrement simplifiées : elles ne tiennent compte que du ratio Dette / PIB noté . Si est la fonction générique (supposée valable pour chaque membre) donnant le taux d’emprunt en fonction du ratio , le coût annuel de la dette s’écrit
La fonction commune « arbitrairement » choisie est une fonction quadratique définie par les trois points (valeurs hypothétiques) :
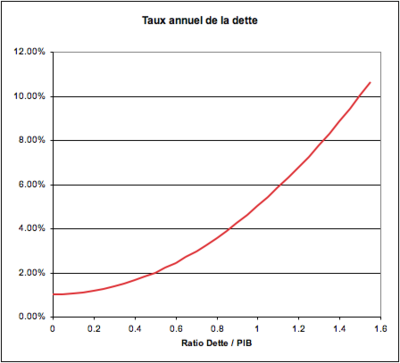
Sur cette base, l’application numérique fournit les résultats suivants :

Ces tableaux indiquent les résultats suivants (à considérer ici comme une simple illustration) :
- Le coût annuel total du financement de la dette pays par pays atteint 964.6 G€.
- Le partenariat permet de réduire ce montant à 837.2 G€, soit un bénéfice de synergie de 127.5 G€ (à l'arrondi près).
- Chaque membre retire un profit dans l’opération (colonne en rouge). Le profit attribué à un membre augmente non seulement avec sa taille, mais également lorsque ses caractéristiques s’écartent de la moyenne : la rémunération est favorable aux « bons » et aux « mauvais » élèves.
- Singulièrement atypique, la dette de la Grèce diminue d’un tiers.
- Certains membres sont parfois rémunérés (coûts négatifs pour une dette positive dans le tableau du milieu, comme c’est le cas pour la Suède) : on peut considérer qu’il s’agit d’une rétribution associée à une forte contribution au bénéfice de synergie.
Note : afin de préserver l’homogénéité des données, certains membres de l’UE n’ont pas été pris en compte dans l’exemple car ils ne font pas partie de l’OCDE (Bulgarie, Chypre, Lettonie, Lituanie, Malte et Roumanie).
Élaboration concrète des résultats précédents :
Partant des dettes nominales , le problème consiste à
- Trouver le paramètre et les inconnues qui minimisent
Les conditions
et la relation
impliquent ainsi
Avec l’hypothèse de convexité de , il en découle que les sont tous égaux à une valeur , qui par la contrainte, ne peut que satisfaire
étant le ratio Dette / PIB de l’ensemble des partenaires, permet de déterminer la solution
puis la répartition stable suivante
Synergie entre les risques
Dans le domaine de la gestion des risques et des effets indésirables provoqués par les aléas, il existe souvent au sein d’un groupe d’acteurs un gisement de synergie qui est peu ou imparfaitement exploité.
Assurance risque
Pour faire face aux catastrophes, les compagnies d’assurances ont développé des mécanismes de mutualisation des risques comme le feu, les risques naturels, la santé, la responsabilité civile, etc. Les clients qui signent un tel contrat préfèrent verser une prime annuelle au lieu d’assumer seuls la probabilité d’un sinistre. Ils estiment ainsi bénéficier d’une part du bénéfice de synergie, même si une partie de ce dernier reste entre les mains de l’assureur.
Il convient de rappeler que le bénéfice de synergie ne se manifeste pas ici en termes d’amélioration de l’espérance de profit : au contraire, l’espérance de coût augmente pour celui qui contracte une police d’assurance, ne serait-ce que pour verser les marges de l’assureur. Par contre, le bénéfice du client se mesure par une augmentation de son utilité, ou plus simplement du bien-être engendré par sa sécurité.
Produit dérivé
Dans le domaine de la finance, les produits dérivés permettent de transférer des risques (relatifs à une évolution des prix futurs) entre un agent qui y est sensible et un autre moins vulnérable. Il s’agit bien ici d’une forme spécifique de cogestion des risques par exploitation d’une synergie particulière entre divers acteurs du marché.
Synergie entre les aléas de résultats
Nombre d’entreprises sont plus ou moins vulnérables à certains phénomènes externes ou exogènes qui influencent leurs résultats financiers et volatilisent les bénéfices ; ces aléas exercent simultanément un effet néfaste sur le coût du capital. Pour y faire face, les entreprises cherchent à diversifier leurs activités. Dans le domaine des aléas météorologiques, un vendeur de parapluies et un vendeur de crèmes solaires constituent un exemple académique qui, malgré sa naïveté, illustre assez bien le problème.
Lorsque les entreprises subissent des effets qui sont essentiellement en opposition les uns aux autres, il est évident que la création d’un partenariat apporte un avantage global. Il est moins intuitif de vérifier la validité de l’assertion précédente lorsque les effets sont statistiquement indépendants, et même lorsqu’ils sont corrélés positivement, c'est-à-dire s’ils ont une propension à s’orienter dans le même sens.
L’intérêt réside moins dans un transfert de risques (typiques des produits dérivés) que dans une mise en commun conduisant à une atténuation ou une dilution des aléas individuels.
Au sein d’un partenariat, les membres sont incités à mettre en œuvre un mécanisme de compensation des aléas dans le but de régulariser leurs résultats respectifs et de réduire les fluctuations des bénéfices. Le bénéfice de synergie ne se manifeste donc pas par une augmentation de l’espérance des résultats respectifs, mais par une réduction de leurs variabilités (ou de leur écarts types).
Mécanisme naturel
Description d’un mécanisme particulier qui, par son mode de répartition, peut être qualifié de « naturel » :
- Choix d’une période commune à tous : ce sont par exemple les bénéfices annuels qui sont visés et le processus de compensation est ainsi mis en œuvre chaque année.
- Choix des variables spécifiques : chaque partenaire détermine une variable aléatoire « objective » d’espérance nulle expliquant au mieux les écarts de son bénéfice noté ; en d’autres termes, la variable est choisie de sorte à minimiser l’écart type de la différence, soit (ce qui nécessite une corrélation positive entre les deux variables).
- Acceptation par tous les partenaires des variables choisies et des modalités de la répartition finale.
- Répartition finale : en fin de période, lorsque les réalisations des variables sont connues de tous, les partenaires exploitent un « pot commun » dans lequel chacun verse (ou retire) le montant , puis le solde du pot (qui peut être négatif) est finalement réparti entre tous en proportion des écarts types respectifs.
Conditions pratiques requises pour la mise en œuvre de ce mécanisme :
- Les variables choisies doivent être objectives : leurs valeurs passées sont connues de tous et aucun partenaire ne doit pouvoir, de quelque façon que ce soit, influencer les réalisations du futur.
- Chacun doit pouvoir constater que les espérances des variables sont nulles (il suffit de retrancher les valeurs espérées).
- Les écarts types de chaque variable et de la somme doivent pouvoir être quantifiés.
Ces conditions sont satisfaites lorsque les variables choisies sont, par exemple, des combinaisons de variables météorologiques dont les paramètres statistiques et les réalisations sont publiés par des services officiels. Il est également possible d’envisager des variables s’exprimant comme des fonctions d’une ou de plusieurs variables : c’est une approche pertinente pour un producteur agricole dont la récolte est sensible à la fois à un excès et à un manque de précipitation.
Ce mécanisme assure à chacun une réduction de sa variabilité. Plus précisément, la variabilité initiale du partenaire caractérisée par diminue d’un certain facteur, la variabilité finale atteignant où est défini par
Note : l’inégalité découle de l’inégalité triangulaire qui se vérifie pour l’écart type.
Chaque partenaire « verse » au pot son résultat et « retire » sa part définie par
- .
La variabilité du résultat passe donc de à dont le rapport est bien le facteur .
Dans la situation particulière où , chaque partenaire retire du pot un montant identique à celui qu’il a versé et il n’y a en fin de compte aucun échange. Elle se produit uniquement dans le cas où toutes les variables sont identiques à un coefficient multiplicatif positif près (coefficient de corrélation égal à 1 pour tout couple). Dans ce cas, il n’y a évidemment aucun bénéfice de synergie possible sur la variabilité, et aucun avantage à retirer d’un partenariat.
Il est facile de vérifier que ce mode de répartition du pot en proportion des peut parfois inciter économiquement un sous-groupe à se séparer de l’ensemble : la stabilité du mécanisme naturel n’est pas assurée dans toutes les situations. Il est d’ailleurs très fréquent de constater l’instabilité de ce mécanisme, ceci d’autant plus que le nombre de partenaires est élevé.
Exemple 1
Considérons 3 partenaires dont les variables sont les mêmes au signe près :
Dans la répartition « naturelle » de la synergie des risques, ils obtiennent un facteur puisque
Si les partenaires 2 et 3 se mettent ensemble, ils obtiennent et éliminent toute vulnérabilité au risque.
En fait, cet exemple n’est pas spécifique au mécanisme naturel car, avec les variables choisies, aucun mécanisme de répartition ne peut être stable. En effet, puisque les partenaires 1 et 3 sont parfaitement opposés et annulent leurs risques, ils ne devraient pas participer à la répartition du pot ; puisque, par symétrie, il en va de même pour les partenaires 2 et 3, il en découle qu’aucun partenaire ne devrait participer à vider le pot, ce qui ne convient pas.
Méthode de construction de variables aléatoires
En partant de vecteurs choisis arbitrairement dans un espace euclidien de dimension finie, il est facile de leur associer une matrice carrée de taille dont les composantes sont les produits scalaires deux à deux. Il est ensuite possible de construire un ensemble de variables aléatoires dont la matrice de covariance est précisément . Sans entrer dans tous les détails :
- est une matrice semi-définie positive qui se diagonalise sous la forme où est une matrice diagonale dont les éléments diagonaux sont les valeurs propres () et où est une matrice orthogonale dont les colonnes contiennent les vecteurs propres correspondants.
- En partant de variables aléatoires supposées indépendantes, d’espérances nulles et de variances respectivement égales aux , les variables définies par ont précisément comme matrice de covariance.
Il est donc possible de proposer un exemple de variables aléatoires en donnant des vecteurs de et en égalisant les produits scalaires et les covariances. Sans confondre les concepts, on identifie les notations pour les vecteurs et les variables associées.
Exemple 2
Considérons ainsi 3 partenaires dont les variables sont associées aux vecteurs suivants :
On vérifie puis .
Pour les partenaires 1 et 2, leurs poids dans la répartition naturelle de sont tous deux égaux à , ce qui conduit à l’attribution globale d’un écart type atteignant alors que l’écart type de la somme est inférieur puisqu’il atteint : ces deux partenaires ayant ainsi intérêt à se séparer du 3e, le mécanisme de répartition naturel est instable dans cette situation.
Alors que le calcul ci-dessus reste un peu laborieux, il est simple de constater dans la situation où les sont du même ordre de grandeur (poids égaux) qu’il suffit que les variables de deux partenaires soient presque en opposition pour qu’ils aient intérêt à se retirer de partenariat.
Mécanisme général
Sans changer les principes de sa mise en œuvre, le mécanisme naturel précédent peut être adapté en modifiant uniquement les poids prédéfinis qui fixent la répartition du pot entre les partenaires. Ces poids ne peuvent être définis qu’en fonction des seules caractéristiques statistiques des variables (comme c’est le cas avec le mécanisme naturel).
Dans une formulation linéaire générale basé sur des poids dont la somme est égale à 1, le processus permet au partenaire de transformer son écart réalisé en un écart effectif défini par
Considérons une formulation dans laquelle chaque partenaire , ayant défini sa propre variable d’espérance nulle, échange avec le pot un montant (à verser si > 0, à retirer sinon) défini par
où la matrice est à déterminer.
À la suite d'une réalisation , le montant final effectif entre les mains du partenaire sera ainsi défini par
et la variable est bien d’espérance nulle.
La somme des montants échangés avec le pot doit être nulle dans tous les cas, ce qui implique la contrainte
où est le vecteur dont les composantes sont toutes identiques à 1.
Afin de tenir compte des tailles respectives des partenaires, considérons des pondérations (vecteur à déterminer).
L’idée consiste à déterminer qui minimise la fonction objectif scalaire
sous la contrainte .
La solution est donnée par
c'est-à-dire
Les éléments d’une colonne de sont identiques et les colonnes sont proportionnelles entre elles.
Il est remarquable de constater que les éléments de ne dépendent pas de la matrice de covariance des .
En fin de compte, le processus permet au partenaire de transformer son écart en un écart défini par
Le mécanisme naturel consiste simplement à choisir .
La détermination des poids nécessite la connaissance de la matrice de covariance des ou, ce qui revient au même, la connaissance de l’écart type de toute somme partielle des .
Problématique de la stabilité
Dans le cadre du mécanisme général, une question importante est la détermination d’une pondération assurant la stabilité du processus de répartition et, le cas échéant, la caractérisation des conditions sous quelles il est possible d’assurer l’existence d’une telle pondération.
Pour la répartition d’un bénéfice de synergie, la question de la stabilité ne se présente pas de la même manière lorsqu’il s’agit de profits ou de risques ; en effet, le caractère additif du premier type de synergie ne se vérifie pas dans le second.
Considérons partenaires dont chacun a choisi sa propre variable . Notons la somme des qui est l’allocation totale du pot à répartir entre les partenaires ; notons encore la covariance des deux variables.
Sous certaines hypothèses (qui ne sont de loin pas respectées dans toutes les situations), la propriété suivante donne une solution aisée à déterminer :
Propriété — Lorsque , une pondération conduisant à un mécanisme stable est donnée par
Supposons sans restreindre la généralité que : dans le cas contraire en effet, le pot est identiquement nul (car l’espérance de est nulle, comme celle des ) et les poids ne jouent ici aucun rôle.
Ainsi, par hypothèse, les indiqués existent, ils sont positifs ou nuls et de somme égale à 1.
Soit un ensemble d’indices correspondant à un sous-groupe. Afin de montrer que le sous-groupe n’a aucun intérêt économique à se séparer de l’ensemble, il suffit de vérifier que l’écart type de leur pot reste supérieur à la somme des écarts types des termes qu’ils retireraient dans le partage du pot de l’ensemble à l’aide les poids indiqués. Si
est le contenu du pot du sous-groupe, il s’agit ainsi de montrer :
Par l’inégalité triangulaire qui se vérifie pour l’écart type :
- .
Cette propriété ne s’applique ainsi qu’aux situations où les corrélations respectives entre les variables des acteurs et leur somme sont positives : ce ne sont donc pas les meilleures conditions pour générer une synergie élevée entre les risques.
En pratique et pour une situation donnée, on peut résumer de la manière suivante le processus de recherche d’une pondération opérationnelle :
- Si , les poids ne jouent pas de rôle : c’est une situation idéale qui est parfaitement stable.
- Dans la situation où , la propriété ci-dessus fournit une pondération stable.
- Avec deux partenaires, il existe toujours une pondération stable :
- La situation respectant les hypothèses de la propriété précédente.
- Le cas contraire où l’un des partenaires (disons le premier) satisfait et l’autre nécessairement : on pose alors et qui est une solution stable apportant un avantage réel à chacun des deux partenaires.
- Dans toute situation, il est possible de formuler un problème dont la solution fournit une pondération stable lorsqu’il en existe une.
La formulation proposée ici passe par la résolution d’un problème de programmation linéaire mais, contrairement à la propriété précédente, le résultat ne donne pas de formules algébriques à partir desquelles les poids des partenaires peuvent être calculés explicitement.
Considérons partenaires dont chacun a choisi sa propre variable . Notons :
et supposons sans restreindre la généralité que .
Soit l’ensemble des sous-groupes non vides parmi les partenaires. À tout élément , notons les scalaires d’appartenance valant 1 si est dans , 0 sinon.
Considérons le problème suivant :
- Trouver les poids qui maximisent
- sous les contraintes
Les contraintes inégalités impliquent que le sous groupe correspondant à n’est pas incité à se séparer de l’ensemble ; ce sont précisément les conditions de stabilité.
Malgré le nombre élevé de contraintes (qui atteint ), ce problème admet toujours une solution bornée :
- est une solution réalisable ;
- lorsque ne comprend que le partenaire ( pour ce seul ), la contrainte inégalité correspondante implique et chaque poids est alors borné ;
- lorsque comprend tous les partenaires ( pour tout ), la contrainte inégalité correspondante implique
Par conséquent :
- Si la solution de ce problème satisfait , elle caractérise des poids garantissant la stabilité.
- Si , il n’y a aucun moyen d’assurer une répartition stable.
- Lorsqu’il n’existe pas de pondération stable, le partenariat risque tôt ou tard d’éclater, ceci quel que soit le mécanisme linéaire de répartition du pot. Pour y remédier, une solution consiste à trouver d’autres partenaires supplémentaires dont les variables contribuent à augmenter la synergie de l’ensemble, ou encore éventuellement d’exclure certains partenaires qui y contribuent peu. D’autres approches envisageables ne résolvent qu’imparfaitement le problème de stabilité :
- Répartition hiérarchique : extraction de certains sous-groupes constitués de partenaires bénéficiant à l’interne d’une synergie élevée (typiquement les sous-groupes incités à quitter le partenariat) ; chaque tel sous-groupe établit ses propres règles de partenariat et de répartition (stable) ; chaque sous-groupe ainsi constitué se comporte comme un partenaire au sein d’un partenariat de niveau supérieur.
- Séparation des partenaires en deux groupes : le groupe constitué de ceux qui satisfont et le groupe constitué des autres. Les poids sont alors définis de la manière suivante :
- Avec ces pondérations, la stabilité de la répartition est assurée au sein de chacun des deux sous-groupes. Les seuls problèmes concernent les incitations à se séparer pour un ensemble de partenaires appartenant collectivement aux deux sous-groupes ; cependant, puisque les partenaires appartenant au groupe ont pu éliminer la totalité de leur variabilité, il faudrait leur proposer un avantage supplémentaire pour qu’ils acceptent de se regrouper avec d’autres partenaires du groupe .
Puisque la variabilité de chacun des partenaires du groupe est nulle, la stabilité au sein de ce groupe est assurée.
Vérifions la stabilité de la répartition au sein du sous-groupe :
En définissant pour tout ,
- .
Considérons un sous-groupe de et notons les scalaires d’appartenance valant 1 si est dans , 0 sinon. Il vient finalement
qui correspond à la condition de stabilité pour le sous-groupe .
- Dans la situation toujours instable présentée comme premier exemple pour le mécanisme naturel, à savoir 3 partenaires dont les variables respectives et le total sont les mêmes au signe près (), la séparation en deux groupes implique , , et . Ainsi, le 3e partenaire (qui est le seul à produire un bénéfice de synergie) se libère totalement de sa variabilité et les deux autres se partagent le pot à parts égales. Il semble évident que cette solution, bien qu’instable, reste la moins risquée pour le partenariat.
 Portail de l’économie
Portail de l’économie







































![{\displaystyle \sum _{i\in A}f_{i}(p_{i}(A))\leqslant \sum _{i\in A}[f_{i}(p_{i})+\lambda ({\hat {p}}_{i}-p_{i})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/429a61f4825aefa14651e9fa3eed66872af89185)































































































































