Kurbadura

Matematikan, kurbadura geometriarekin estuki erlazionaturiko kontzeptua da. Intuitiboki, kurba bat lerro zuzen bat izatetik edo gainazal bat plano bat izatetik desbideratzen diren neurria da.

Kurbei dagokienez, eredu kanonikoa zirkuluarena da, bere erradioaren alderantzizko zenbakiko kurbadura duena. Zirkulu txikiagoak zakarrago tolesten dira eta, beraz, kurbadura handiagoa dute. Kurba diferentzial baten puntu bateko kurbadura bere zirkunferentzia ukitzailearen kurbadura da. Lerro zuzen baten kurbadura zero da. Ukitzailearen kasuan, aldiz, puntu bateko kurbadura eskalar baten bidez adierazten da, zenbaki erreal positibo baten bidez, hain zuzen ere.

Espazio euklidear batean txertatuta dauden gainazalen kasuan, kurbaduraren kontzeptua konplexuagoa da, gainazalean norabide bat hautatzearen araberakoa baita. Horrek kurbadura maximoa, gutxieneko kurbadura eta batezbesteko kurbadura kontzeptuetara garamatza.

Historia

Tractatus de configurationibus qualitatum et motuum^[1] liburuan, Nicole Oresmek, XIV. mendeko filosofo eta matematikariak, kurbadura kontzeptua proposatu zuen zuzentasunetik desbideratzeko neurri gisa. Zirkuluen kurbadura alderantziz proportzionala denez erradioarekiko, ideia hau beste kurba batzuetara hedatzen saiatzen da Oresme, magnitude aldagarri gisa^[2].

Parametrizazioa

Kurba baten kurbadura kalkulatu aurretik, ezinbestekoa da kurbaren parametrizazioa lortzea. Izan bedi ${\displaystyle C}$,  planoko zein espazioko kurba bat. ${\displaystyle C}$-ren parametrizazio bat funtzio bat da, zenbaki errealen multzoko tarte batetik espaziora zein planora doana, non tarte horretako balio bakoitzari ${\displaystyle C}$ -ko puntu bat esleitzen zaion. Horrez gain, kurbadura ondo definitu ahal izateko, parametrizazioa definitzen duen funtzioak jarraitua eta deribagarria izan beharko du. Orduan, parametrizazioa ${\textstyle \gamma :[a,b]\longrightarrow \mathbb {R^{n}} }$ erako aplikazio bat izango da, ${\displaystyle n=2}$ izanik planoko kurben kasuan eta ${\displaystyle n=3}$ espazioko kurben kasuan.

Planoko kurben kasuan, aplikazioa mota honetakoa izango da:

${\displaystyle \gamma :[a,b]\longrightarrow \mathbb {R^{2}} }$

${\displaystyle t\mapsto \gamma (t)=(x(t),y(t))}$

Adibidez, erradioa 1 luzerakoa duen zirkunferentziaren parametrizazioa hurrengoa izango da:

${\displaystyle \gamma :[0,2\pi ]\longrightarrow \mathbb {R^{2}} }$

${\displaystyle \theta \mapsto \gamma (\theta )=(cos(\theta ),sin(\theta ))}$

Deribatua

Izan bedi ${\displaystyle \gamma (t)=(x(t),y(t))}$ kurba parametrizatua. Orduan, bere deribatua honako eran definituko dugu: ${\displaystyle \gamma '(t)=(x'(t),y'(t))}$.

Hau da, koordenatu bakoitzeko ${\displaystyle t}$-rekiko deribatua egingo dugu.

Norma

Izan bedi ${\displaystyle \gamma (t)=(x(t),y(t))}$ kurba parametrizatua. Bere norma euklidearra honako eran definituko dugu: ${\displaystyle \lVert \gamma (t)\rVert ={\sqrt {x(t)^{2}+y(t)^{2}}}}$.

Hau da,  koordenatu guztien karratuen baturaren erro karratua eginez kalkulatuko dugu.

Kurba lauak

Intuitiboki, kurbadura kontzeptuak zera islatzen du: kurba baten edozein puntutan kurba horren norabidea zenbatean aldatzen den; beraz, zenbat eta kurbadura handiagoa izan, orduan eta gehiago aldatzen da kurbaren norabidea^[3]. Definizio formala nahi izanez gero, arku luzeraz parametrizatutako kurba baten puntu zehatz bateko kurbadura, da puntu horretako bektore ukitzailearen deribatuaren luzera da.

Kurbaduraren definizioak eta haren karakterizazioek eskatzen dute kurba jarraitutasunez diferentziagarria izatea, etengabe aldatzen den ukitzaile bat baitu; halaber, kurba bi aldiz diferentziagarria izan behar du, tartean diren mugak eta bektore ukitzailearen deribatua ondo definituta dagoela ziurtatzeko.

Kurbaduraren karakterizazioa unitate bektore ukitzailearen deribatuaren arabera ez da zirkunferentzia ukitzailearen arabera egindako definizioa bezain intuitiboa, baina kurbadura kalkulatzeko formulak errazago ondoriozta daitezke. Beraz, eta zinematikan ere erabiltzen denez, kurbaduraren definizio baterako, maiz ematen da aurreneko karakterizazio hori.

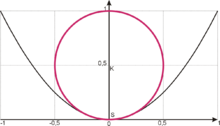
Zirkunferentzia ukitzailea

Historikoki, kurbadura zirkunferentzia ukitzailearen bidez definitu izan ohi da, zirkunferentzia hori baita, puntu zehatz horretan, kurba ondoen hurbiltzen duen zirkunferentzia. Zehazki, kurba batean ${\displaystyle P}$ puntu bat emanda, kurbaren beste edozein ${\displaystyle Q}$ puntuk (edo batzuetan lerro batek) ${\displaystyle Q}$ puntutik pasatzen den eta ${\displaystyle P}$-n kurbari ukitzailea den zirkulu bat definitzen du. Egonez gero, zirkunferentzia ukitzailea ${\displaystyle Q}$-k ${\displaystyle P}$-ra jotzen dueneko zirkunferentziaren limitea da. Kurbadura kurbadura-erradioaren alderantzizkoa da; hau da,

${\displaystyle \kappa ={\frac {1}{R}}}$

non ${\displaystyle R}$ kurbadura-erradioa^[4] den (zirkulu osoak kurbadura hori du, ${\displaystyle 2\pi R}$-ko luzeeran ${\displaystyle 2\pi }$-ko biraketa gisa irakur daiteke).

Definizio hau zaila izan daiteke erabiltzeko eta formuletan adierazteko. Horregatik, beste definizio baliokide batzuk sortu eta erabiltzen dira.

Arku-parametrizazioa

Edozein kurba diferentziagarri arku-luzeraz^[5] parametriza daiteke. Kurba lau baten kasuan, horrek esan nahi du:

${\textstyle \gamma (s)=(x(s),y(s))}$.

${\displaystyle \lVert \gamma '\rVert ={\sqrt {x'(s)^{2}+y'(s)^{2}}}=1}$

Horrek esan nahi du bektore ukitzailea ${\displaystyle \mathrm {T} (s)=(x'(s),y'(s))}$, norma bat duela eta, beraz, bektore ukitzailea unitarioa da.

Kurba bi aldiz diferentziagarria bada, hau da, ${\textstyle x}$ eta ${\textstyle y}$-ren bigarren deribatuak existitzen badira, orduan, ${\textstyle \mathrm {T} (s)}$ deribatua existitzen da. ${\textstyle \mathrm {T} (s)}$ bektorea kurbarekiko normala da, bere norma kurbadura ${\displaystyle \kappa (s)}$ da eta kurbaren zentrorantz orientatuta dago.

${\displaystyle \mathrm {T} (s)=\gamma '(s)}$

${\displaystyle \lVert \mathrm {T} (s)\rVert ^{2}=1(konstantea)\Rightarrow \mathrm {T} '(s).\mathrm {T} (s)=0}$

${\displaystyle \kappa (s)=\lVert \mathrm {T} '(s)\rVert =\lVert \gamma ''(s)\rVert ={\sqrt {x''(s)^{2}+y''(s)^{2}}}}$

Are gehiago, kurbaren erradioa honako hau da (${\displaystyle \kappa (s)\neq 0}$ dela suposatuta):

${\displaystyle R(s)={\frac {1}{\kappa (s)}}}$

Eta kurbaduraren zentroa kurbaren zuzen normalean dago:

${\displaystyle C(s)=\gamma (s)+{\frac {1}{\kappa (s)}}\mathrm {T} '(s)}$

(Kurbadura zero denean, kurbaduraren zentroa ez dago ${\displaystyle \mathbb {R} ^{2}}$ planoan. Kasu horretan “infinituan” kokatuta dagoela deritzogu.)

${\displaystyle \mathrm {N} (s)}$ bektore unitarioa da eta ${\displaystyle \mathrm {T} (s)}$-tik lortzen dugu, erlojuaren orratzen kontrako noranzkoan ${\displaystyle {\frac {\pi }{2}}}$ graduko errotazioa eginez. Orduan,

${\displaystyle \mathrm {T} '(s)=k(s)\mathrm {N} (s)}$

${\displaystyle k(s)=\pm \kappa (s)}$ izanik. ${\displaystyle k(s)}$ zenbaki erreala kurbadura orientatua da, planoaren eta kurbaren orientazioaren araberakoa dena. ${\displaystyle s\longrightarrow -s}$ aldagai aldaketak ${\displaystyle k(s)}$ kontrako zeinua duen arku-bidezko parametrizazioa ematen digu.

Parametrizazio orokorra

Izan bedi ${\displaystyle \gamma (t)=(x(t),y(t))}$ bi aldiz diferentziagarria den planoko kurba baten parametrizazioa. Parametizazio hori erabiliz, kurbadura honako hau da:

${\displaystyle \kappa (s)={\frac {\left\vert x'y''-y'x''\right\vert }{(x'^{2}+y'^{2})^{3/2}}}}$

Koordenatu gabeko era batean adierazteko:

${\displaystyle \kappa ={\frac {\left\vert det(\gamma ',\gamma '')\right\vert }{\lVert \gamma '\rVert ^{3}}}}$

Formula hauek arku-luzera bidezko parametrizazioaren kasutik atera daitezke. Aurreko parametrizazioaren baldintzaren ondorioz, arku-bidezko funtzioaren ${\displaystyle s}$ parametroa, ${\displaystyle t}$ parametroaren funtzio diferentziagarri monotonoa da. Eta alderantziz, ${\displaystyle t}$ ${\displaystyle s}$-ren funtzio monotonoa da. Halaber, ${\displaystyle s}$-ren ordez ${\displaystyle -s}$ idatziz (behar izanez gero) funtzioak gorakorrak izango dira eta deribatua positiboa. Aurreko ataleko notazioa eta katearen erregela erabiliz,

${\displaystyle {d\gamma \over dt}={ds \over dt}\mathrm {T} }$

Bi aldeetan normak hartuz,

${\displaystyle {dt \over ds}={1 \over \lVert \gamma '\rVert }}$

Kurbadura ${\displaystyle \mathrm {T} }$-ren ${\displaystyle s}$-rekiko deribatuaren norma da. Goiko formula eta katearen erregela erabiliz, aurreko deribatua eta bere norma ${\displaystyle \gamma '}$ eta ${\displaystyle \gamma ''}$-ren bidez adierazi daitezke. Horrela, arku-luzera bidezko ${\displaystyle s}$ parametroa ezabatzea lortzen da.

Funtzio baten grafoa

${\displaystyle y=f(x)}$ funtzio baten grafoa kurba parametrizatuaren kasu berezia da:

${\displaystyle x=t}$

${\displaystyle y=f(t)}$

${\displaystyle x}$-ren lehen eta bigarren deribatuak ${\displaystyle 1}$ eta ${\displaystyle 0}$ direnez, hurrenez hurren, aurreko kurbaduraren formulak honela sinplifikatzen dira:

${\displaystyle \kappa ={\frac {\left\vert y''\right\vert }{(1+y'^{2})^{3/2}}}}$

Grafoaren malda (edo funtzioaren deribatua) txikia denean, bigarren deribatua kurbaduraren hurbilpen ona da. Zehatzago, goi-borne asintotikoa erabiliz,

${\displaystyle k(x)=y''(1+O(y'^{2})).}$

Fisika eta Ingeniaritzan ohikoa da kurbadura bigarren deribatuaren bidez hurbiltzea; esate baterako, kurba elastikoetan edota uhinaren ekuazioan. Honek aukera ematen digu ez-linealak diren sistemak linealtzat hartzeko.

Koordenatu polarrak

Kurba bat koordenatu polarretan adierazita dago, hurrengo eran parametrizatuta dagoenean: ${\textstyle x=r(\theta )\cos(\theta )}$, ${\textstyle y=r(\theta )\sin(\theta )}$, non ${\displaystyle r}$ erradioa eta ${\displaystyle \theta }$ angelua diren.

Kurba bat koordenatu polarretan adierazita dagoenean kurbadura honako hau da:

${\displaystyle \kappa (\theta )={\frac {\left\vert r^{2}+2r'^{2}-rr''\right\vert }{(r^{2}+r'^{2})^{3/2}}}}$

Adibideak

Erabilgarria izan daiteke aurreko ataletan definitutako formulek, adibide sinpleetan, benetan emaitza berdinak ematen dituztela egiaztatzea.

Zirkunferentzia

Aurretik azaldu dugun bezala, ${\displaystyle r}$ erradioko zirkunferentzia baten ohiko parametrizazioa ${\displaystyle \gamma (t)=(r\sin(t),r\cos(t))}$. Kurbaduraren formula jarraituz

${\displaystyle k(t)={\frac {r^{2}\sin ^{2}t+r^{2}\cos ^{2}t}{(r^{2}\cos ^{2}t+r^{2}\sin ^{2}t)^{3/2}}}={\frac {1}{r}}}$

Espero dugun bezala, kurbaduraren erradioa eta zirkunferentziaren erradioa berdinak dira. Are gehiago, kurbaduraren zentroa zirkunferentziaren zentroa da.

Zirkunferentzia arku-luzera bidezko parametrizazioa kalkulatzeko erraza duen kasu berezi bat da. Bereziki,

${\displaystyle \gamma (s)={\Bigl (}r\cos {\frac {s}{r}},r\sin {\frac {s}{r}}{\Bigr )}}$

Arku-luzerazko parametrizazioa da, izan ere

${\displaystyle \gamma '(s)={\Bigl (}-\sin {\frac {s}{r}},\cos {\frac {s}{r}}{\Bigr )}}$ adierazpenaren norma ${\displaystyle 1}$en berdina da. Parametrizazio honi elkartutako kurbadurak balio bera du, aurreko formulan bere burua ${\displaystyle r^{3}}$-gatik zatitzerakoan izendatzaile eta zenbakitzailean balio hori lortzen baitugu.

Erreferentziak

Kanpo estekak

• Datuak: Q214881
• Multimedia: Illustrations for curvature and torsion of curves / Q214881