Steinerscher Satz
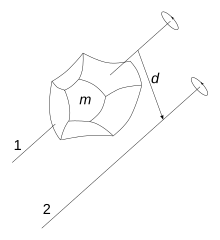
Drehachse 1 geht durch den Schwerpunkt des Körpers der Masse .
Drehachse 2 ist um den Abstand d verschoben.
Der Steinersche Satz (auch Satz von Steiner, Steiner-Regel, Satz von Huygens-Steiner oder Parallelachsen-Theorem[1]) dient der Berechnung des Trägheitsmomentes eines starren Körpers für parallel verschobene Drehachsen. Der Satz geht auf Untersuchungen von Jakob Steiner und Christiaan Huygens zurück.
Das Trägheitsmoment eines Körpers hängt von der Lage der Drehachse ab. Ist das Trägheitsmoment bezüglich einer Drehachse durch den Massenmittelpunkt bekannt, so kann mit dem Steinerschen Satz das Trägheitsmoment für alle Drehachsen, die parallel zu dieser sind, berechnet werden.
Der Satz wird auch verwendet, um Flächenträgheitsmomente von Balken-Querschnitten zu bestimmen.
Anwendung auf Trägheitsmomente
Trägheitsmomente sind meistens für Drehachsen durch den Massenmittelpunkt tabelliert. Falls das Trägheitsmoment für eine dazu parallele Drehachse benötigt wird, kann der Steinersche Satz angewendet werden und das Trägheitsmoment ergibt sich zu:
Dabei ist das Trägheitsmoment des Körpers mit Masse bezüglich der Drehachse , die durch seinen Massenmittelpunkt (praktisch gleich dem Schwerpunkt) geht und parallel mit Abstand zur Drehachse liegt.
Bei Anwendung des Steinerschen Satzes ist zweierlei zu beachten:
- Das Trägheitsmoment eines Körpers ist dann am geringsten, wenn die Drehachse durch den Schwerpunkt geht. Das folgt daraus, dass der Steinersche Anteil stets positiv ist, wenn man eine Verschiebung vom Schwerpunkt weg durchführt.
- Mit mehrmaliger Anwendung des Steinerschen Satzes kann das Trägheitsmoment zu einer beliebigen parallelen Achse berechnet werden, auch wenn das anfangs gegebene Trägheitsmoment nicht durch den Massenmittelpunkt geht.
Anwendung auf Flächenträgheitsmomente
Liegt der Flächenschwerpunkt eines Körper-Querschnitts nicht im Ursprung des Koordinatensystems, kann sein Flächenträgheitsmoment mit dem Steinerschen Satz berechnet werden:
Für wird der Abstand des Flächenschwerpunktes zum Ursprung quadriert, mit der Fläche des Querschnitts multipliziert und auf das (tabellarisch erfasste) Flächenträgheitsmoment addiert. Es ist ersichtlich, dass bei der Steiner-Term wegfällt.
Praktisch ist, dass man mit diesen Formeln komplexe (z. B. T-Träger) in einfache Körper (z. B. Rechtecke) aufteilen kann, deren Flächenträgheitsmoment bereits bekannt ist.
Für gilt dann beispielsweise:
- ,
wobei die Fläche der Figur ist und bis die durch die Zerlegung entstandenen Teilflächen sind.
Verallgemeinerung auf Trägheitstensoren
Hat ein Körper eine Masse und, bezogen auf den Schwerpunkt, den Trägheitstensor , so ergibt sich der Trägheitstensor in einem um den Vektor parallel verschobenen Koordinatensystem durch die Summe aus und dem Trägheitstensor eines Massenpunktes der Masse und dem Ortsvektor :
d. h.
wobei
bzw. in Summenkonvention mit dem total antisymmetrischen ε-Tensor
Daher gilt auch
Durch die Verschiebung kann es vorkommen, dass die Achsen des neuen Koordinatensystems nicht mehr mit den Hauptträgheitsachsen durch den neuen Punkt zusammenfallen.
Herleitung

Betrachtet man einen starren Körper in einem Koordinatensystem, dessen Ursprung mit seinem Massenmittelpunkt übereinstimmt und legt die Rotationsachse parallel zur z-Richtung, so ist das Trägheitsmoment bezüglich dieser Achse definiert als
- .
Wobei die Summe über alle Massenpunkte des Körpers läuft, der Ort des jeweiligen Massenpunktes mit bezeichnet ist und die Rotationsachse auf der Geraden parallel zur z-Achse durch den Punkt liegt.
Ausmultiplizieren der Klammern führt auf
Der erste Term entspricht dem Trägheitsmoment der Rotationsachse durch den Massenmittelpunkt (und parallel zur z-Achse). Der zweite und dritte Term sind Null, da sie der Definition des Massenmittelpunktes und entsprechen und dieser nach Voraussetzung im Ursprung liegt: .[2] Der vierte Term gibt nach Pythagoras gerade das Abstandsquadrat der Rotationsachse zum Ursprung multipliziert mit der Gesamtmasse des betrachteten Körpers an. Schreibt man den Abstand als , so ergibt sich der Steinersche Satz als
- .
Literatur
- Alfred Böge: Technische Mechanik: Statik – Dynamik – Fluidmechanik – Festigkeitslehre. Springer DE, ISBN 978-3-8348-8107-6 (eingeschränkte Vorschau in der Google-Buchsuche).
- Wolfgang Demtröder: Experimentalphysik 1: Mechanik und Wärme. Springer DE, 2008, ISBN 978-3-540-79295-6, S. 146 (eingeschränkte Vorschau in der Google-Buchsuche).
- Christian Spura: Technische Mechanik 2. Elstostatik, Springer Vieweg, Wiesbaden 2019, ISBN 978-3-658-19978-4
- Karl-Eugen Kurrer: Geschichte der Baustatik. Auf der Suche nach dem Gleichgewicht, Ernst und Sohn, Berlin 2016, S. 89, ISBN 978-3-433-03134-6




























![{\displaystyle J_{B}=\sum _{i}m_{i}\left[(x_{i}-x_{B})^{2}+(y_{i}-y_{B})^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/febe4952056a6c023b5ec5883190eda1ed0171ef)


















