Höhenschnittpunkt

Der Höhenschnittpunkt (auch: Orthozentrum) eines Dreiecks ist der Schnittpunkt seiner drei Höhen, d. h. der Lote zu den Dreiecksseiten durch die gegenüberliegenden Ecken. Der Höhenschnittpunkt ist einer der vier klassischen ausgezeichneten Punkte des Dreiecks.

In der Skizze sind die Höhen mit [AH_a], [BH_b] und [CH_c] bezeichnet. Ist das gegebene Dreieck ABC spitzwinklig, so befindet sich der Höhenschnittpunkt H innerhalb des Dreiecks. Hat das Dreieck dagegen einen stumpfen Winkel (also einen Winkel über 90°), so liegt H außerhalb. Im rechtwinkligen Fall schließlich stimmt H mit dem Scheitel des rechten Winkels überein.

Beweis

Zum Beweis, dass sich alle drei Höhen des Dreiecks ${\displaystyle ABC}$ in einem Punkt schneiden, zeichnet man die Parallelen zu den Dreiecksseiten durch die gegenüberliegenden Ecken, sodass ein größeres Dreieck ${\displaystyle A'B'C'}$ entsteht. Je zwei der vier Teildreiecke des neuen Dreiecks bilden ein Parallelogramm. In einem Parallelogramm sind gegenüberliegende Seiten gleich lang. Daher sind die Seiten des neuen Dreiecks doppelt so lang wie die entsprechenden Seiten des ursprünglichen Dreiecks. Die Höhen des ursprünglichen Dreiecks stimmen daher mit den Mittelsenkrechten (Streckensymmetralen) des neuen Dreiecks überein. Da sich die Mittelsenkrechten eines Dreiecks in einem Punkt schneiden (→ siehe Umkreis), muss dies auch für die Höhen des Ausgangsdreiecks gelten.

Umgekehrt kann man dem Dreieck ${\displaystyle A'B'C'}$ das Dreieck ${\displaystyle ABC}$ als Dreieck seiner Mittelparallelen einbeschreiben. Damit fällt der Umkreismittelpunkt des ursprünglichen Dreiecks mit dem Höhenschnittpunkt des einbeschriebenen Dreiecks zusammen.

Verallgemeinerung in der synthetischen Geometrie

Die im Beweis mitbewiesene Äquivalenz des Höhenschnittpunktsatzes zum Mittellotensatz, lässt sich in der synthetischen Geometrie auf affine Translationsebenen mit einer Orthogonalitätsrelation verallgemeinern, falls jede Strecke der Ebene eine Mitte hat, d. h. falls die Ebene das affine Fano-Axiom erfüllt. Dann kann aus der Existenz dieser Schnittpunkte für beliebige Dreiecke geschlossen werden, dass die Translationsebene eine pappussche Ebene ist. Insofern wird der Höhenschnittpunktsatz in der synthetischen affinen Geometrie als Axiom behandelt.

Eigenschaften

• Das Dreieck aus den Fußpunkten H_a, H_b und H_c der Höhen bezeichnet man als das Höhenfußpunktdreieck des Dreiecks ABC. Ist das Dreieck ABC spitzwinklig, dann ist der Höhenschnittpunkt H des Dreiecks ABC der Inkreismittelpunkt des Höhenfußpunktdreiecks; ist das Dreieck ABC stumpfwinklig, dann ist der Höhenschnittpunkt H des Dreiecks ABC ein Ankreismittelpunkt des Höhenfußpunktdreiecks.

• Die Produkte der Höhenabschnitte sind gleich:

${\displaystyle {\overline {AH}}\cdot {\overline {HH_{a}}}={\overline {BH}}\cdot {\overline {HH_{b}}}={\overline {CH}}\cdot {\overline {HH_{c}}}}$.

• Der Höhenschnittpunkt liegt – wie der Schwerpunkt und der Umkreismittelpunkt – auf der Eulerschen Geraden.

• Die Fußpunkte der Höhen und die Mittelpunkte der „oberen Höhenabschnitte“ (jeweils zwischen dem Höhenschnittpunkt und einer Ecke) liegen auf dem Feuerbach-Kreis.

• Spiegelt man den Höhenschnittpunkt an den drei Seiten des Dreiecks, so liegen die Bildpunkte auf dem Umkreis.

Koordinaten

Höhenschnittpunkt eines Dreiecks (Orthozentrum, ${\displaystyle X_{4}}$)
Trilineare Koordinaten	${\displaystyle \sec \alpha \,:\,\sec \beta \,:\,\sec \gamma }$
Baryzentrische Koordinaten	${\displaystyle \tan \alpha \,:\,\tan \beta \,:\,\tan \gamma }$

Orthozentrische Quadrupel

Gegeben sei ein Dreieck ${\displaystyle ABC}$ und sein Höhenschnittpunkt ${\displaystyle H}$. Dann gelten die folgenden Aussagen:

• Der Höhenschnittpunkt des von drei der vier Punkte ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$ und ${\displaystyle H}$ gebildeten Dreiecks ist jeweils der vierte Punkt.
• Die von drei der vier Punkte ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$ und ${\displaystyle H}$ gebildeten Dreiecke haben kongruente Umkreise.

Die vier Punkte ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$ und ${\displaystyle H}$ werden auch als orthozentrisches Quadrupel bezeichnet.

• 
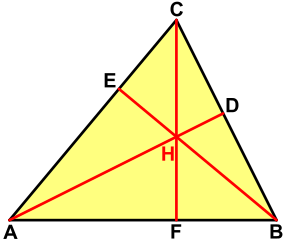  Figur 1
• 
  Figur 2
• 
  Figur 3
• 
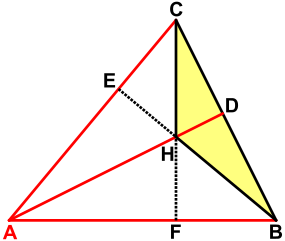  Figur 4

Beweis:

Die erste Aussage resultiert unmittelbar aus den Figuren 1 bis 4.

Der Beweis der zweiten Aussage basiert auf Figur 5. Ohne Beschränkung der Allgemeinheit wird die Kongruenz der Umkreise für die beiden Dreiecke ${\displaystyle ABC}$ und ${\displaystyle ABH}$ gezeigt.

Im Dreieck ${\displaystyle ABE}$ ergänzen sich der rot markierte Winkel ${\displaystyle \angle HBF}$ und der Winkel ${\displaystyle \angle FAE}$ zu 90°. Ebenso ergänzen sich im Dreieck ${\displaystyle CAF}$ der rot markierte Winkel ${\displaystyle \angle ECH}$ und der Winkel ${\displaystyle \angle FAE}$ zu 90°. Hieraus folgt, dass die beiden rot markierten Winkel gleich groß sind.

Der Punkt ${\displaystyle P}$ ist der zweite Schnittpunkt des Umkreises des Dreiecks ${\displaystyle ABC}$ mit der verlängerten Dreieckshöhe durch ${\displaystyle C}$. Der rot markierte Winkel ${\displaystyle \angle ECH}$ und der grün markierte Winkel ${\displaystyle \angle FBP}$ sind als Umfangswinkel am Kreisbogen über ${\displaystyle AP}$ gleich groß. Damit sind auch der rot markierte Winkel ${\displaystyle \angle HBF}$ und der grün markierte Winkel ${\displaystyle \angle FBP}$ gleich groß. Folglich sind nach dem Kongruenzsatz WSW dann auch die rechtwinkligen Dreiecke ${\displaystyle BHF}$ und ${\displaystyle PBF}$ kongruent. Somit sind nach dem Kongruenzsatz SWS auch die Dreiecke ${\displaystyle ABH}$ und ${\displaystyle BAP}$ kongruent, also sind auch ihre Umkreise kongruent.

Da demnach der Umkreis des Dreiecks ${\displaystyle BAP}$ auch der des Dreiecks ${\displaystyle ABC}$ ist und die Umkreise der Dreiecke ${\displaystyle ABH}$ und ${\displaystyle BAP}$ kongruent sind, haben auch die Dreiecke ${\displaystyle ABC}$ und ${\displaystyle ABH}$ kongruente Umkreise. Damit ist die zweite Aussage bewiesen.

Spezialfall der ersten Aussage:

• Sind drei der vier Punkte ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$ und ${\displaystyle H}$ Eckpunkte eines rechtwinkligen Dreiecks, so fällt der jeweils vierte Punkt mit einem der drei anderen zusammen.^[1]

Literatur

• H. Schupp: Elementargeometrie. UTB Schöningh 1977, ISBN 3-506-99189-2, S. 50.
• Wendelin Degen und Lothar Profke: Grundlagen der affinen und euklidischen Geometrie, Teubner, Stuttgart, 1976, ISBN 3-519-02751-8
• Max Koecher, Aloys Krieg: Ebene Geometrie, 3. Aufl., Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3

Weblinks

• http://www.mathe-werkstatt.de/titel.htm interaktives Java-Applet, das die Kurve der Höhenschnittpunkte anzeigt

Einzelnachweise

1. ↑ Günter Aumann: Kreisgeometrie. Eine elementare Einführung. Springer Spektrum, Springer-Verlag Berlin Heidelberg 2015, ISBN 978-3-662-45305-6, Seiten 29 und 30