Elektrický odpor
| Elektrický odpor | |
|---|---|
| Název veličiny a její značka | Elektrický odpor R |
| Hlavní jednotka SI a její značka | ohm |
| Definiční vztah | |
| Dle transformace složek | skalární |
| Zařazení jednotky v soustavě SI | odvozená |
Elektrický odpor resp. Rezistance je reálnou částí komplexní impedance elektrického obvodu, bránící průchodu elektrického proudu. Hodnota elektrického odporu závisí na materiálu, průřezu, délce i teplotě vodiče. Odpor vodičů se vzrůstající teplotou stoupá (kladný teplotní součinitel elektrického odporu), kdežto odpor polovodičů se vzrůstající teplotou klesá (záporný teplotní součinitel elektrického odporu). Převrácená hodnota elektrického odporu je fyzikální veličina, která se nazývá elektrická vodivost.
Impedance
Reaktance a rezistance elektrického obvodu tvoří komplexní impedanci :
- ,
kde
- je impedance; měří se v ohmech.
- je rezistance; měří se v ohmech.
- je reaktance; měří se v ohmech.
- je imaginární jednotka
Výpočet
Elektrický odpor lze určit jednak pomocí Ohmova zákona:
- ,
kde je napětí na koncích vodiče v jednotkách [V] a je proud procházející vodičem v jednotkách [A],
jednak pomocí materiálových vlastností vodiče:
- ,
kde je měrný elektrický odpor materiálu vodiče, je délka vodiče v jednotkách a je průřez vodiče v jednotkách ,
a jednak pomocí závislosti elektrického odporu na teplotě:
- ,
kde je odpor vodiče při teplotě 20 °C, je teplotní součinitel elektrického odporu a je teplotní rozdíl. Za teplot blížících se absolutní nule může elektrický odpor u některých látek klesnout na nulu. Takovým látkám se říká supravodiče.
Ztráty
Teče-li vodičem s odporem proud dochází k přeměně elektrické energie na teplo a tím k výkonovým ztrátám, které lze vyjádřit vztahem:
- ,
kde je ztráta výkonu v jednotkách [W].
Tento jev se využívá u zařízení jako žárovka (emituje světlo žhavící spirály) nebo elektrické topení (emituje teplo žhavící spirály), nicméně je nežádoucí při přenosu energie. Obvyklým způsobem redukce výkonových ztrát je přenos výkonu na vyšších napěťových hladinách či užívání vodičů o větším průřezu či paralelně zapojených.
Měření
Elektrický odpor se měří digitálním nebo analogovým měřícím přístrojem, Ohmovou metodou, srovnávací metodou a substituční metodou. K napájení obvodu s odporem musíme použít vždy stejnosměrný proud, protože měřením při střídavém napájení bychom nezjistili velikost elektrického odporu, ale hodnotu impedance celého obvodu. Při měření elektrických odporů působí na měřící obvod různé rušivé vlivy, které mohou ovlivňovat zejména měření velmi malých nebo velmi velkých odporů. Mezi tyto rušivé vlivy patři mimo jiné parazitní indukčnost a parazitní kapacita odporu.
Rozdělení
Z hlediska velikosti můžeme elektrické odpory rozdělit na:
- malé: do 1 Ω – přechodové odpory, odpor vodičů pro vedení elektrického proudu
- střední: 1 Ω až 1 MΩ – běžné hodnoty rezistorů pro zapojení v elektronice
- velké: nad 1 MΩ – izolační odpory, odpory pro vysoká napětí
Pro představu: 10 metrů vodiče, který vám přivádí proud do zásuvky 230 V~, má odpor 0,12 Ω. Klasická 40 W žárovka do stolní lampičky má 1,32 kΩ když svítí (za studena má 132 Ω). Odpor předřazený doutnavce ve vypínači u zásuvky má velikost 220 kΩ. Izolační odpor v domácích rozvodech by měl mít odpor nad 1 GΩ.
Ohmova metoda
Ohmova metoda měření elektrického odporu je klasický způsob měření, při němž vypočítáváme velikost odporu měřené zátěže pomocí Ohmova zákona. Podle toho, zda měříme odpor s malým nebo velkým odporem, volíme vhodný způsob měření. Vybereme-li vhodnou metodu, lze zanedbat příslušnou chybu měření, protože bude vzhledem k výsledné hodnotě malá (nemusíme uvažovat vnitřní odpor voltmetru nebo ampérmetru) a použít přímo naměřené hodnoty (viz níže).
Platí vztah:
- – úbytek napětí na měřeném odporu
- – proud protékající měřeným odporem
Zapojení pro malé odpory

Pokud bychom vypočítali velikost odporu pouze jako podíl hodnot naměřených voltmetrem a ampérmetrem, dopustili bychom se určité chyby výpočtu, protože ampérmetr naměří vyšší proud (o ten, který protéká voltmetrem). Pokud však použijeme tuto metodu pro zjištění odporu malých hodnot, lze tuto chybu měření zanedbat (voltmetr má velký vnitřní odpor a jím protékající proud bude zanedbatelný ve srovnání s proudem protékajícím malým odporem ).
V takovém zjednodušeném výpočtu lze využít vztahu (použijeme přímo hodnoty naměřené voltmetrem a ampérmetrem):
Pokud bychom však chtěli zahrnout i proud protékající voltmetrem, platil by pro velikost měřeného odporu přesnější výpočet (musíme však předem znát vnitřní odpor voltmetru pro daný napěťový rozsah):
Ampérmetr měří proud, který prochází měřeným odporem a zároveň proud, který prochází voltmetrem.
Voltmetr měří přímo napětí na zátěži . Nyní bude vzorec pro měřený odpor vypadat takto:
Pro proud protékající voltmetrem platí:
- – vnitřní odpor voltmetru pro daný napěťový rozsah.
Pro výslednou velikost odporu tak platí:
Zapojení pro velké odpory
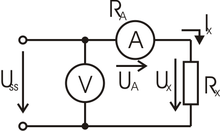
Pokud bychom vypočítali velikost odporu pouze jako podíl hodnot naměřených voltmetrem a ampérmetrem, dopustili bychom se určité chyby výpočtu, protože voltmetr naměří vyšší napětí (o napětí na ampérmetru). Pokud však použijeme tuto metodu pro zjištění odporu velkých hodnot, lze tuto chybu měření zanedbat (ampérmetr má malý vnitřní odpor a napětí na něm bude zanedbatelné ve srovnání s napětím na velkém odporu ).
V takovém zjednodušeném výpočtu lze využít vztahu (použijeme přímo hodnoty naměřené voltmetrem a ampérmetrem):
Pokud bychom však chtěli zahrnout i napětí na ampérmetru, platil by pro velikost měřeného odporu přesnější výpočet (musíme však předem znát vnitřní odpor ampérmetru pro zvolený rozsah):
Ampérmetr měří přímo proud tekoucí zátěží . Voltmetr měří součet úbytků napětí na ampérmetru i na zátěži.
Měřený odpor se vypočte:
Pro úbytek napětí na ampérmetru platí:
- – vnitřní odpor ampérmetru pro zvolený rozsah.
Pro velikost měřeného odporu můžeme napsat vztah:
Srovnávací metoda
Při měření odporu srovnávací metodou porovnáváme neznámý odpor s odporem známé velikosti.
Zapojení pro malé odpory

Velikost neznámého odporu zjistíme změřením úbytků napětí na jednotlivých rezistorech. Proud v obvodu musí být konstantní.
Protože oběma rezistory teče stejný proud, platí:
Pro relativní chybu měření platí:
Čím více se budou hodnoty a sobě přibližovat, tím větší bude chyba měření. Bude-li , bude chyba metody prakticky zanedbatelná. Tato metoda je velmi přesná, velikost odporu můžeme zjistit s přesností až na několik setin procenta.
Zapojení pro velké odpory
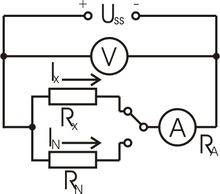
Rezistory jsou zapojené paralelně. Napětí musí být po celou dobu měření konstantní.
Velikost odporu se zjišťuje srovnáním proudů tekoucích jednotlivými rezistory. Platí:
Pro relativní chybu měření platí:
Čím menší bude vnitřní odpor ampérmetru, tím menší bude chyba měření. Měření bude přesnější, když budou hodnoty a blíže u sebe.
Pro tuto metodu měření je vhodné, aby byl měřený odpor v rozsahu 1 kΩ až 1 MΩ.
Odkazy
Související články
Literatura
- NEČÁSEK, Sláva. Radiotechnika do kapsy. Praha: SNTL, 1981. 43 s. Kapitola Základní elektrotechnické vztahy.
- SEDLÁK, Bedřich; ŠTOLL, Ivan. Elektřina a magnetismus. Praha: ACADEMIA, 2002. 650 s. ISBN 80-200-1004-1.
- Elektrotechnická měření. Praha: nakladatelství BEN - technická literatura, 2002. 255 s. ISBN 80-7300-022-9.
Externí odkazy
 Obrázky, zvuky či videa k tématu elektrický odpor na Wikimedia Commons
Obrázky, zvuky či videa k tématu elektrický odpor na Wikimedia Commons















![{\displaystyle [m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b649f5418f2ac84d66063f41319368b0926ccec4)

![{\displaystyle [mm^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2f792975dd869d6a223b93648e7656d42edcfff)







![{\displaystyle \left[\Omega ;V,A\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24c6fd0a5b70d83056fd6a05290d2fa707f23093)































